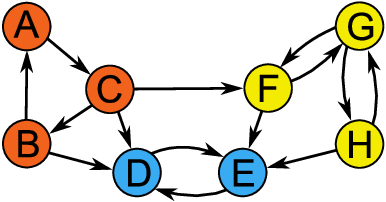
Strongly Connected Components
SCCs란?
방향 그래프 (Directed Graph)에서, 정점들의 집합 중 모든 정점 쌍 사이에 경로가 존재하는 경우, 이 집합을 Strongly Connected Component, SCC라고 한다. 즉, SCC 내의 모든 정점은 서로 도달 가능하다.
한편, SCC는 그래프를 분석하고 이해하는 데 유용하게 사용된다. 예를 들어, 소셜 네트워크에서 SCC는 서로 밀접하게 연결된 사용자 그룹을 나타낼 수 있다. 또한, SCC는 그래프를 더 작은 부분으로 나누어 분석하는 데에도 사용될 수 있다.
SCC 분해: 그래프를 SCC로 어떻게 나눌까?
흥미로운 질문은, 주어진 그래프를 어떻게 SCC로 분해할 수 있을까? 하는 것이다. 직관적으로 생각해 보면, 만약 A 그룹에서 B 그룹으로 가는 간선만 존재하고, B 그룹에서 A 그룹으로 가는 간선이 없다면, B 그룹에서 시작하는 탐색을 통해 SCC를 찾을 수 있을 것이다.
 |
| How do we find SCC? |
하지만, 다음 상황에서 B 집단에 속하는 요소를 어떻게 고를 것인가? 만약 A 집단에서 시작한다면 DFS가 전체 집단을 return하므로 SCC를 찾지 못할 것이다.
놀랍게도 현재 DFS를 단 2번 실행하여 SCC를 찾는 방법이 존재한다. 그 알고리즘에 대해 자세히 살펴보겠다.
DFS를 두 번만 사용하여 SCC를 찾는 방법은 다음과 같다.
- 임의의 정점에서 DFS 수행: 그래프의 임의의 정점에서 시작하여 DFS를 수행한다. 이때 각 정점의 방문 순서와 종료 순서를 기록한다.
- 간선 역전: 그래프의 모든 간선의 방향을 역전시킨다.
- 종료 시간 기준 DFS 수행: 첫 번째 DFS에서 기록한 종료 시간을 기준으로 내림차순으로 정점을 정렬한다. 정렬된 순서대로 각 정점에서 DFS를 수행한다. 이때 각 DFS 탐색에서 방문한 정점들의 집합이 하나의 SCC를 구성한다.
왜 이 방법이 작동할까?
이 방법의 핵심 아이디어는 SCC 그래프의 특징을 이용하는 것이다. SCC 그래프는 각 SCC를 하나의 정점으로 표현한 그래프이다.
 |
| DAG characteristic |
- Lemma 1 : SCC 그래프는 방향 비순환 그래프 (DAG) 이다.
- Lemma 2 : 간선 (u, v)에 대해 항상 u의 종료 시간이 v의 종료 시간보다 크다.
Lemma1에서 DAG가 아니라고 가정하면, 사이클이 생기게 되므로 SCC가 하나의 정점이라는 전제에 위배된다.
Lemma2는 DFS를 공부하며 증명한 적이 있다. DAG이므로 반드시 성립하는 가정이다.
따라서 첫 번째 DFS를 수행하면 A그룹의 종료 시간이 B그룹의 종료 시간보다 크게 나타난다.이후 간선을 역전시키고 A그룹에서 DFS를 수행하게 되면 A그룹에서는 나가는 간선이 없으므로 오직 connected component끼리만 묶이게 된다. 따라서 이를 반복하면 SCCs를 찾을 수 있다.
예시:
 |
| How do we find SCC? |
다시 앞의 그래프를 생각해 보자.
- 정점 A에서 DFS를 시작하면, 방문 순서는 A-B-C-D-E-F이고, 종료 순서는 F-E-D-C-B-A이다.
- 간선을 역전시킨다.
- 종료 시간이 가장 큰 A에서 DFS를 수행하면, SCC {A, B, C}만 서로 연결된다.
- A, B, C를 제외하고 다음으로 D에서 DFS를 수행하면, SCC {D, E, F}만 서로 연결된다.
결론:
DFS를 최대 두 번만 사용하여 SCC를 찾는 방법은 SCC 그래프의 DAG 특징을 이용한 효율적인 알고리즘이다. 지금까지 배운 개념들을 활용한 놀라운 발상이었다. 이 방법은 그래프 알고리즘 분야에서 중요한 알고리즘 중 하나로 꼽히기에 어떻게 개념들이 연결되는지 잘 이해할 필요가 있다.
추천글:
[알고리즘] Graph algorithm - Depth First Search, Topological ordering
(https://hyeondev.blogspot.com/2024/10/graph-algorithm-depth-first-search.html)