오류 기반 학습: 선형 회귀 모델
들어가며
선형 회귀는 데이터 분석 및 기계 학습에서 널리 사용되는 기법으로, 변수 간의 선형 관계를 모델링하여 예측 또는 분석에 활용한다. 이번 포스팅에서는 선형 회귀의 기본 개념부터 오류 함수, 오류 표면, 최소 제곱 최적화, 경사 하강법까지 심층적으로 다룰 것이다.
선형 회귀: 변수 간의 선형 관계 모델링
선형 회귀는 독립 변수 (설명 변수)와 종속 변수 (반응 변수) 간의 관계를 선형 함수로 모델링하는 것이다. 예를 들어, 사무실 크기와 임대 가격 간의 관계를 분석한다고 가정하자. 사무실 크기가 증가할수록 임대 가격은 어떻게 변화할까? 이러한 관계를 선형 회귀를 사용하여 모델링할 수 있다.
 |
| linear regression example |
선형 회귀 모델의 장점
선형 회귀 모델은 다음과 같은 장점을 갖는다.
- 설명력: 변수 간의 관계를 명확하게 보여준다. 사무실 크기가 임대 가격에 미치는 영향을 파악할 수 있다.
- 예측력: 훈련 데이터에 없는 값에 대해서도 예측을 수행할 수 있다. 예를 들어, 730 평방 피트 사무실의 임대 가격을 예측할 수 있다.
- 단순성: 선형 함수를 사용하기 때문에 이해하고 구현하기 쉽다.
수학적 모델
선형 회귀 모델은 다음과 같은 수학적 모델로 표현된다.
y = mx + b
여기서 y는 종속 변수, x는 독립 변수, m은 기울기, b는 y 절편이다.
단순 선형 회귀 모델
단순 선형 회귀 모델은 하나의 독립 변수를 사용하여 종속 변수를 예측하는 모델이다. 예를 들어, 사무실 크기만을 사용하여 임대 가격을 예측하는 모델을 생각해 보자.
이 모델은 다음과 같이 표현된다.
임대 가격 = w[0] + w[1] * 크기
여기서 w[0]는 y 절편, w[1]은 기울기이다.
 |
| many combination of w[0], w[1] |
위 그림과 같이 w[0]과 w[1]의 조합은 다양하게 나타난다. 하지만 우리가 원하는 것은 가장 정확하게 관계를 표현할 수 있는 w[0]과 w[1] 조합이다. 이걸 어떻게 하면 formal하게 측정할 수 있을까?
그렇게 등장한 것이 바로 error function이다.
error function은 모델의 예측값과 실제값 간의 차이를 측정하는 함수이다. 오류 함수를 사용하여 모델의 성능을 평가하고, 최적의 모델을 찾을 수 있다. linear regression에서 주로 사용되는 error function은 'SSE(Sum of Squared Error)'이다. 본 포스팅에서도 SSE를 기준으로 알아보고자 한다.
제곱 오차 합 (SSE): 오류 표면 생성
제곱 오차 합 (Sum of Squared Errors, SSE)은 error function 중 하나로, 예측값과 실제값 간의 차이의 제곱을 합한 것을 2로 나눈 것이다.
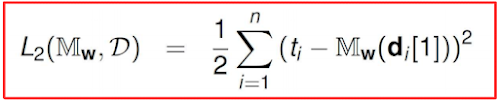 |
| Sum of Squared Error |
 |
| SSE calculation example |
위와 같이 SSE를 계산하였을 때 최소가 되는 w[0]와 w[1] 조합이 가장 최적의 조합이라고 할 수 있다.
하지만 여기에도 문제가 있다. 바로 모든 w[0], w[1] 조합을 계산하여 비교하는 것이 현실적으로 불가능하다는 점이다.
그래서 우리는 다른 접근을 하고자 한다. 먼저, SSE를 사용하여 error surface를 생성할 수 있다. error surface는 각 가중치 조합에 대한 SSE 값을 나타낸다.
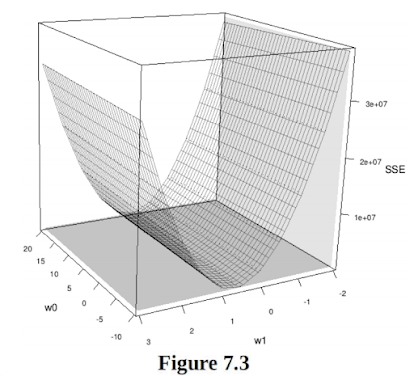 |
| error surface |
여기서 error surface의 최저점은 최적의 가중치 조합을 나타낸다. 즉 우리는 convex(볼록)한 지점만 선별하여 w[0], w[1] 조합을 찾는다면 훨씬 효과적으로 계산할 수 있다. 이렇게 가중치 조합을 찾는 방법을 최소 제곱법이라 한다.
최소 제곱 최적화: 최적의 가중치 찾기
앞서 언급한 바와 같이, 최소 제곱 최적화는 오류 표면의 최저점을 찾아 최적의 가중치 조합을 찾는 방법이다. 미적분학에서 배웠던 개념을 적용하면 이 지점에서 w[0], w[1]에 대한 편미분 값은 0이 되어야 한다.
 |
| partial derivatives |
이번 시간에는 simple linear regression model이므로, local minima 문제가 발생하지 않지만 변수가 많은 경우 최저점을 찾지 못하는 경우가 발생할 수 있다. 그래서 경사하강법이 등장하였다. 이 부분에 대해서는 다음 시간에 구체적으로 다뤄보고자 한다.
최소제곱법을 이용한 선형회귀의 구체적인 계산 과정은 선형대수학 시간에 다룬 바 있으므로 자세한 내용은 다음을 참고하도록 하자.
마치며
이번 포스팅에서는 선형 회귀 모델의 기본 개념부터 오류 함수, 오류 표면, 최소 제곱 최적화, 편미분까지 심층적으로 다루었다. 다음 포스팅에서는 경사 하강법을 사용하여 최적의 가중치를 찾는 방법에 대해 알아보도록 하겠다.
추천글:
[인공지능개론] Naive Bayes Model
(https://hyeondev.blogspot.com/2024/10/naive-bayes-model.html)
[선형대수학] 최소자승법(Linear square problem)
(https://hyeondev.blogspot.com/2024/05/linear-square-problem.html)
[인공지능개론] similarity based learning - the nearest neighbor algorithm
(https://hyeondev.blogspot.com/2024/10/similarity-based-learning-nearest.html)
