[컴퓨터비전개론] Overview of 3D Computer Vision - Homogeneous Transformation Matrix (HTM)

3차원 비전: 3D 형상과 변환, 그리고 동차 변환 행렬(HTM)

지난 시간까지 2차원 이미지의 패턴을 인식하고 신경망을 통해 세상을 이해하는 방법을 탐구했다면, 이제는 한 차원 더 나아가 우리를 둘러싼 3차원(3D) 세계를 컴퓨터 비전이 어떻게 다루는지 알아볼 차례다. 카메라라는 2차원 센서로 얻은 영상으로부터 3차원 공간에 존재하는 객체의 크기, 위치, 그리고 자세(방향)를 정확히 파악하는 것은 로봇 공학, 자율 주행, 증강 현실, 의료 영상 분석 등 첨단 기술의 심장과도 같다.

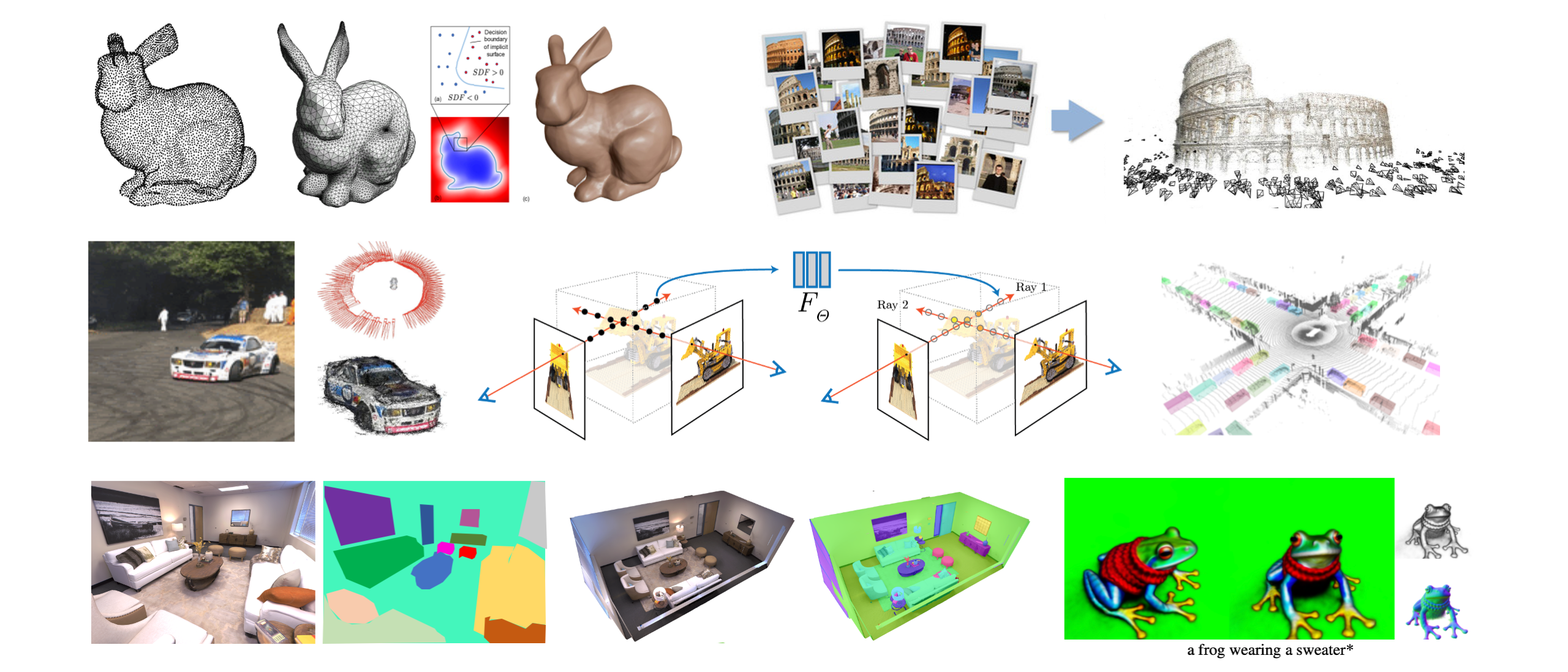3D Computer Vision

이번 시간에는 컴퓨터 비전에서 3D 형상(Geometry)과 변환(Transformation)이 왜 그토록 중요한지, 그리고 이들을 다루는 핵심 도구인 동차 변환 행렬(Homogeneous Transformation Matrix, HTM)이 무엇인지, 기본적인 내용부터 심도 있게 파헤쳐 보고자 한다.

컴퓨터 비전과 3D: 왜 중요하고, 무엇을 다루나?

컴퓨터 비전의 궁극적인 목표 중 하나는 단순히 이미지를 "보는" 것을 넘어, 그 안에 담긴 3차원 공간과 객체들을 "이해"하는 것이다. 우리가 스마트폰으로 AR 필터를 쓰거나, 자율주행차가 주변 환경을 인식하는 것 모두 3D 공간에 대한 이해가 바탕이 된다.

무엇을 이해해야 할까?

3차원 형상(3D Geometry): 3차원 공간상의 점(point), 선(line), 면(plane)과 같은 기하학적 요소들의 모양, 크기, 상대적 위치 등을 의미한다.
좌표계(Coordinate System / Frame): 3차원 공간에서 어떤 대상의 위치와 자세를 기술하기 위한 기준틀이다. 예를 들어, "내 앞에 있는 컵"의 위치는 나를 기준으로 한 좌표계, 방을 기준으로 한 좌표계, 또는 지구를 기준으로 한 좌표계 등 다양한 좌표계에서 다르게 표현될 수 있다. {A}, {B}와 같이 중괄호로 특정 좌표계를 표시하곤 한다.
변환(Transformation): 한 객체가 3차원 공간에서 움직이거나(이동, 회전), 혹은 한 좌표계에서 표현된 객체의 정보를 다른 좌표계 기준으로 바꾸는 과정을 수학적으로 기술하는 것이다.

카메라 캘리브레이션(Camera Calibration)은 카메라 내부의 광학적 특성과 카메라가 세상 어느 곳에 어떤 방향으로 놓여있는지를 알아내어 3차원 점이 2차원 이미지에 어떻게 맺히는지 그 관계를 규명하는 과정이다. (다음 시간에 다룰 내용)

객체 추적(Object Tracking)은 시간에 따라 움직이는 객체의 3차원 위치와 자세를 영상에서 연속적으로 알아내는 기술이다. 이 모든 작업의 근간에는 3D 형상과 변환에 대한 수학적 모델링이 깔려있다. 이번 시간에 다룰 내용이 바로 이에 관한 내용이다.

변환의 기초: 회전(Rotation)과 병진(Translation) 🔄➡️

3차원 공간에서 강체(rigid body, 모양과 크기가 변하지 않는 물체)의 움직임은 크게 병진 이동(Translation)과 회전(Rotation)으로 나눌 수 있다.

병진 이동 (Translation):
가장 간단한 변환으로, 객체가 특정 방향으로 일정한 거리만큼 평행하게 이동하는 것을 의미한다. 3차원 공간의 한 점 $ p=(p_{x},p_{y},p_{z})^{T}$를 병진 벡터 $ t=(t_{x},t_{y},t_{z})^{T}$만큼 이동시킨 새로운 점 ${p}'$는 단순히 벡터 덧셈으로 표현된다:
\[{p}'=p+t=\begin{pmatrix}p_{x}+t_{x}\\p_{y}+t_{y}\\p_{z}+t_{z}\\\end{pmatrix}\]

Translation

회전 (Rotation):
객체가 특정 점이나 축을 중심으로 각도만큼 돌아가는 것을 의미한다. 3차원 공간에서의 회전은 3×3 크기의 회전 행렬(Rotation Matrix) $R$로 표현된다. 점 $p$를 원점을 기준으로 회전시킨 새로운 점 ${p}'$는 다음과 같이 행렬 곱으로 나타낸다:
\[{p}'=Rp\]
회전 행렬 R은 몇 가지 중요한 특징을 가진다:

직교 행렬(Orthogonal Matrix): $R^{T}R=RR^{T}=I$ (여기서 $I$는 단위 행렬, $R^{T}$는 $R$의 전치 행렬). 이는 회전 변환이 길이와 각도를 보존한다는 의미이며, $$R^{-1}$=$ $R^{T}$임을 뜻한다.
행렬식(Determinant) 값: $det(R)=+1$. (만약 -1이면 반사(reflection) 변환을 포함한다.)

Rotation

문제는 회전과 병진을 순차적으로 적용할 때 ${p}'=Rp+t$와 같이 행렬 곱과 벡터 덧셈이 섞여 있어 여러 변환을 연속적으로 적용하기가 번거롭다는 점이다. 만약 변환이 10번 연속된다면 수식이 매우 복잡해질 것이다. 이를 깔끔하게 하나의 행렬 연산으로 통합할 방법은 없을까?

만능 도구, 동차 변환 행렬 (Homogeneous Transformation Matrix, HTM) 🛠️

이러한 고민을 해결해주는 마법 같은 도구가 바로 동차 변환 행렬(Homogeneous Transformation Matrix, HTM)이다. HTM은 회전과 병진을 하나의 $4 \times 4$ 행렬로 통합하여 표현함으로써 여러 변환을 단순히 행렬 곱으로 연속 적용할 수 있게 해준다.

동차 좌표계 (Homogeneous Coordinates):
HTM을 사용하기 위해서는 먼저 3차원 좌표를 4차원 동차 좌표로 확장해야 한다. 3차원 점 $ (p_{x},p_{y},p_{z})$는 동차 좌표에서 $ (p_{x},p_{y},p_{z},1)^{T}$와 같이 마지막에 1을 추가한 4차원 벡터로 표현된다. (방향만을 나타내는 벡터는 $ (v_{x},v_{y},v_{z},0)^{T}$로 표현하여 병진 이동의 영향을 받지 않도록 할 수 있다.)
HTM의 구조:
HTM T는 3×3 회전 행렬 R과 3×1 병진 벡터 t를 사용하여 다음과 같이 정의된다:
\[ T=\begin{bmatrix}R&T\\0^{T}&1\\\end{bmatrix}=\begin{bmatrix}r_{00}&r_{01}&r_{02}&t_{x}\\r_{10}&r_{11}&r_{12}&t_{y}\\r_{20}&r_{21}&r_{22}&t_{z}\\0&0&0&1\\\end{bmatrix}\]

여기서 $R$은 회전을, $t$는 병진을 나타내며, 아랫줄의 $0^{T}$는 1×3 영벡터 (0, 0, 0)이다. 마지막 요소는 보통 1이다 (이 부분은 투영 변환 등에서 다른 값을 가질 수 있지만, 강체 변환에서는 1이다).
이제 동차 좌표로 표현된 점 ${p}_{homo}'$에 HTM $T$를 곱하면 변환된 점 ${p}_{homo}''$를 얻을 수 있다:
\[{p}_{homo}''=T{p}_{homo}'\Rightarrow\begin{bmatrix}{p}_{x}''\\{p}_{y}''\\{p}_{z}''\\1\\\end{bmatrix}=\begin{bmatrix}R&t\\0^{T}&1\\\end{bmatrix}\begin{bmatrix}{p}_{x}'\\{p}_{y}'\\{p}_{z}'\\1\\\end{bmatrix}=\begin{bmatrix}Rp_{cartesian}'+t\\1\\\end{bmatrix}\]
결과적으로 변환된 점의 3차원 좌표는 $p_{cartesian}''=Rp_{cartesian}'+t $ 가 되어, 회전 후 병진 이동이 하나의 행렬 곱으로 표현된 것을 볼 수 있다!

Homogeneous Transformation Matrix

이때 "객체는 스케일을 제외하고는 그 형태가 변하지 않는다는 특성(homogeneous)을 가진다"는 설명은, 여기서 'homogeneous'가 동차 좌표계를 사용한다는 의미와 강체 변환의 특성(형태 불변)이 혼합된 설명이다. 정확히는, 강체 변환을 나타내는 HTM은 스케일 변화를 포함하지 않으며(즉, 스케일은 1), 객체의 형태와 크기를 그대로 보존한다. '동차(homogeneous)'라는 용어 자체는 변환이 직선을 직선으로, 평면을 평면으로 매핑하는 등의 성질을 유지한다는 의미도 내포한다.

HTM의 역할과 특징:

좌표계 간 관계 정의: HTM $ T^{A}_{B}$는 프레임 {B}로 표현된 점을 프레임 {A} 기준으로 변환하거나, 프레임 {B}가 프레임 {A}에 대해 가지는 상대적인 위치와 자세(pose)를 나타낸다. 즉, 는 프레임 {B}(물체)의 점 $ P_{B}$를 프레임 {A}(공간)의 점 $ P_{A}$로 변환하는 것을 의미한다.
Rigid Body Motion
강체 변환 표현: HTM은 강체의 회전과 병진을 동시에, 그리고 우아하게 표현한다.
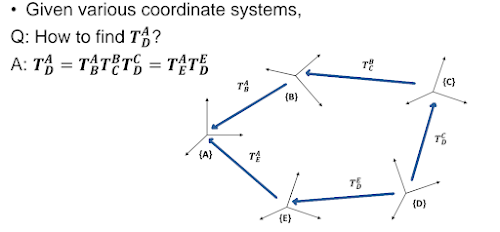
연속 변환의 편리성 (HTM 연쇄 곱셈): 여러 좌표계 변환을 거쳐야 할 때, HTM들을 순서대로 곱하기만 하면 된다. 예를 들어, 프레임 {C}의 점을 프레임 {A}로 변환하는 $T^{A}_{C}$는 $T^{A}_{B}$ (B를 A로 변환)와 $T^{B}_{C}$ (C를 B로 변환)의 곱으로 표현된다: 주의할 점은 행렬 곱의 순서다. 이므로, 변환 순서를 정확히 지켜야 한다.
Chain of HTM
역변환: 프레임 {A}에서 프레임 {B}로의 변환 $T^{B}_{A}$는 $T^{A}_{B}$의 역행렬이다: $T^{B}_{A}=(T^{A}_{B})^{-1}$. HTM의 역행렬은 다음과 같이 비교적 간단히 구할 수 있다 (회전행렬 R이 직교행렬이므로 $R^{-1}=R^{T}$): \[(T^{A}_{B})^{-1}=\begin{bmatrix}R&t\\0^{T}&1\\\end{bmatrix}^{-1}=\begin{bmatrix}R^{T}&-R^{T}t\\0^{T}&1\\\end{bmatrix}\]

Inverse HTM

HTM의 실제 활용: 어디에 어떻게 쓰이나? 🏥🤖

HTM은 컴퓨터 비전, 로보틱스, 컴퓨터 그래픽스 등 3차원 공간을 다루는 거의 모든 분야에서 핵심적으로 사용된다.

의료 영상 및 수술 네비게이션:
- 영상 등록(Image Registration): CT, MRI 등 서로 다른 시점이나 다른 장비로 촬영된 의료 영상들을 정합하여 정보를 통합하는 데 사용된다. 예를 들어, CT 영상의 뼈 정보와 MRI 영상의 연조직 정보를 하나의 좌표계로 통일하여 의사가 더 정확한 진단을 내릴 수 있도록 돕는다.
- 수술 네비게이션(Surgical Navigation): 수술 중인 환자의 해부학적 구조(의료 영상 기준)와 수술 도구의 실시간 위치 및 자세를 일치시켜 의사에게 네비게이션 정보를 제공한다. 예를 들어, 환자 몸속의 특정 지점을 정확히 찾아가야 할 때, 수술 도구의 끝이 현재 영상 어디에 해당하는지를 보여준다. 다음 그림 와 같은 수식은 이러한 관계를 나타낸다.
  - $F^{O}_{D}$: 광학 트래커 좌표계 {O}에서 본 수술 도구 {D}의 자세 (트래커가 실시간 측정)
  - $F^{P}_{O}$: 환자 좌표계 {P}에서 본 광학 트래커 {O}의 자세 (캘리브레이션을 통해 얻음, $ (F^{P}_{O})^{-1}$ )
  - $F^{I}_{P}$: 의료 영상 좌표계 {I}에서 본 환자 {P}의 자세 (수술 전 영상과 환자를 정합하여 얻음)
  - 이들을 순차적으로 곱하면 $F^{I}_{D}$, 즉 의료 영상 좌표계 {I}에서 본 수술 도구 {D}의 자세를 알 수 있게 된다.
로보틱스: 로봇 팔의 각 관절 각도로부터 로봇 손 끝(end-effector)의 위치와 자세를 계산하는 순기구학(Forward Kinematics), 반대로 원하는 손 끝 자세를 만들기 위한 관절 각도를 계산하는 역기구학(Inverse Kinematics)에 HTM이 필수적으로 사용된다. 이동 로봇의 경우 자신의 위치와 방향을 추정(Localization)하고 지도를 작성(Mapping)하는 SLAM 기술에도 HTM이 핵심 역할을 한다.
증강 현실(AR) 및 가상 현실(VR): 현실 세계 영상 위에 가상 객체를 자연스럽게 올려놓거나, 사용자의 움직임에 따라 가상 세계 시점을 변경하기 위해서는 카메라(또는 사용자 머리)의 3차원 자세를 정확히 알아야 하며, 이는 HTM으로 표현되고 계산된다.

HTM은 어떻게 구하나?: 등록 기법 살짝 맛보기 (세부 내용은 추후)

실제 응용에서는 두 좌표계 간의 HTM, 즉 T를 알아내는 과정이 매우 중요하다. 이를 등록(Registration)이라고 하며, 다양한 방법이 존재한다.

쌍점 등록 (Paired-Point Registration, PPR):
두 좌표계에서 서로 대응되는 점들의 쌍(paired points)을 알고 있을 때 사용한다. 예를 들어, 프레임 {A}의 점들 {$p_{A,i}$}와 이에 대응하는 프레임 {B}의 점들 {$p_{B,i}$}가 주어졌을 때, $p_{A,i}\approx T^{A}_{B}p_{B,i}$를 만족하는 최적의 $T^{A}_{B}$를 찾는 것이다. 모든 점에 대해 오차가 정확히 0이 되기는 어렵기 때문에, 보통 점들 사이의 거리 오차 제곱의 합(Fiducial Registration Error, FRE)을 최소화하는 $T^{A}_{B}$를 찾는다. 이 과정에는 최소 제곱법(Least-Squares Method)이나 특이값 분해(Singular Value Decomposition, SVD)와 같은 수학적 기법이 활용된다.

반복 최근접 점 정합 (Iterative Closest Point, ICP):
점들 간의 명시적인 대응 관계를 모를 때, 주로 두 개의 점 구름(point cloud) 데이터를 정합하는 데 사용된다. 한 점 구름의 각 점에 대해 다른 점 구름에서 가장 가까운 점을 찾아 임시적인 대응 관계를 만들고, 이를 바탕으로 PPR과 유사하게 T를 추정한다. 이 T를 적용하여 점 구름을 이동시킨 후, 다시 최근접 점을 찾는 과정을 오차가 충분히 줄어들 때까지 반복한다. ICP는 초기 추정치에 민감할 수 있어, 대략적인 정렬 후 ICP를 사용하여 정밀도를 높이는 방식이 선호되기도 한다.

결론: 3차원 세계를 이해하는 첫걸음

컴퓨터 비전이 2D 이미지를 넘어 3D 세계를 이해하고 상호작용하기 위해서는 3차원 형상과 변환에 대한 깊이 있는 이해가 필수적이다. 그중에서도 동차 변환 행렬(HTM)은 회전과 병진을 하나의 행렬로 통합하여 복잡한 3차원 변환을 체계적이고 효율적으로 다룰 수 있게 해주는 강력한 도구이다. 로봇의 움직임을 제어하고, 의료 영상을 분석하며, 가상 객체를 현실에 증강시키는 등 수많은 첨단 기술의 이면에는 바로 이 HTM이 있다.

오늘 우리는 HTM의 기본 개념부터 실제 응용, 그리고 HTM을 결정하는 방법까지 살펴보았다. 물론 3D 컴퓨터 비전의 세계는 훨씬 더 깊고 방대하지만, HTM까지 배웠으니 앞으로 펼쳐질 더 흥미로운 주제들을 알아가기에 충분한 준비가 되었다고 생각한다. 최근 2025 구글 I/O에서 공개된 구글 글래스 등 AR/VR의 세계가 머지 않았다고 느껴지기에, 앞으로도 기회가 된다면 3D 컴퓨터 비전에 대해 종종 다뤄보고자 한다.

[컴퓨터비전개론] Object Recognition - Template Matching, Fourier Descriptor

[컴퓨터비전개론] Convolutional Neural Network (CNN)