[시스템프로그래밍] Working with Cache - Memory Mountain, Optimization

시스템 프로그래밍 관점에서 캐시(Cache) 파헤치기: 메모리 계층 구조와 성능 최적화

지난 포스팅에서는 메모리 계층 구조(Memory Hierarchy)를 간략히 살펴보면서, 왜 우리 시스템에 캐시(Cache)라는 존재가 필요한지, 그리고 그 위치는 어디쯤인지 감을 잡을 수 있었다. 오늘은 여기서 한 걸음 더 나아가, 시스템 프로그래밍 관점에서 이 캐시라는 녀석을 좀 더 깊이 있게 탐구해 보고자 한다. 단순히 '빠른 메모리'라는 표면적인 이해를 넘어, low-level에서 캐시가 실제로 어떻게 동작하고 시스템 성능에 어떤 영향을 미치는지 파악하는 것은 상위 엔지니어로 성장하기 위한 필수 과정이라고 생각한다. 이 포스팅은 캐시에 대한 전반적인 개념과, 특히 행렬 곱셈(Matrix Multiplication) 예제를 통해 캐시 최적화의 중요성을 체감하는 데 초점을 맞출 것이다.

1. 캐시(Cache)의 기본 개념 및 기능: 왜 필요하고, 어떻게 동작하는가?

캐시는 컴퓨터 시스템의 핵심 구성 요소 중 하나로, CPU와 메인 메모리 사이의 속도 차이를 메우기 위한 고속의 작은 메모리이다. 메인 메모리는 크고 저렴하지만 상대적으로 느린 반면, 캐시는 작고 비싸지만 매우 빠르다.

핵심 아이디어는 메인 메모리의 특정 부분 집합(subset)을 미리 캐시에 가져다 놓는 것(caching)이다. 이때, 메인 메모리는 여러 개의 블록(blocks)으로 나뉘어 있다고 생각할 수 있으며, 데이터는 이 블록 단위로 캐시와 메인 메모리 사이를 오간다.

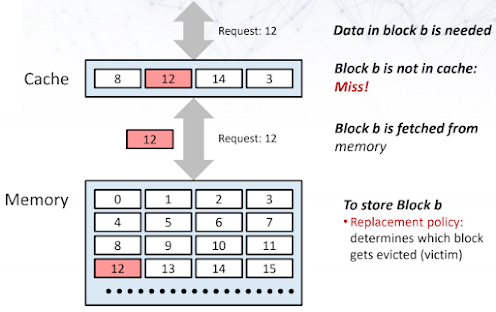
Caching idea

CPU가 어떤 데이터 블록 b를 필요로 할 때, 다음과 같은 두 가지 상황이 발생한다:

캐시 히트 (Cache Hit): 만약 블록 b가 이미 캐시 내에 존재한다면, CPU는 느린 메인 메모리까지 갈 필요 없이 매우 빠른 캐시에서 데이터를 즉시 가져올 수 있다. 이는 접근 지연 시간(access latency)을 크게 줄여 프로그램 실행 속도를 눈에 띄게 향상시킨다.

Cache Hit

캐시 미스 (Cache Miss): 반대로 블록 b가 캐시에 없다면, 이는 캐시 미스가 발생했음을 의미한다. 이 경우, 해당 블록 b는 메인 메모리에서 캐시로 우선 로드(load)되어야 하고, 그 후에야 CPU가 접근할 수 있다. 당연히 캐시 히트보다 훨씬 긴 시간이 소요된다.

Cache Miss

이러한 캐싱 원리는 CPU 캐시뿐만 아니라 우리 주변의 다양한 시스템에서 활용된다. 예를 들어, 웹 브라우저가 웹 페이지를 캐싱하여 로딩 속도를 높이는 것이나, 운영체제가 파일의 일부를 버퍼 캐시에 저장해두는 것, 심지어 가상 메모리 시스템에서 페이지를 캐싱하는 것 모두 같은 원리이다. 우리가 주로 다룰 CPU 캐시는 통상적으로 64바이트(bytes) 블록 크기로 동작하며, 이를 캐시 라인(cache line)이라고도 부른다.

2. Intel Core i7의 캐시 구조 들여다보기 (예시)

현대의 CPU는 단일 캐시가 아닌, 여러 단계로 구성된 계층적 캐시 구조(Hierarchical Cache Structure)를 가진다. 대표적인 예로 Intel Core i7 프로세서의 온칩(on-chip) 캐시 구조를 살펴보자. (프로세서 모델마다 세부 사항은 다를 수 있지만, 일반적인 구조를 이해하는 데 도움이 될 것이다.)

Intel Core i7 Cache Hierarchy

L1 캐시 (Level 1 Cache):
- CPU 코어에 가장 가깝고, 따라서 가장 빠르다.
- 명령어만 저장하는 L1 i-cache (instruction cache)와 데이터만 저장하는 L1 d-cache (data cache)로 분리되어 있는 경우가 많다 (하버드 아키텍처의 변형).
- 각각 32KB 정도의 크기를 가지며, 8-way set associative 구조를 가진다. (associativity에 대해서는 추후 더 자세히 다룰 기회가 있을 것이다.)
- 접근 지연 시간은 약 4 사이클(cycles) 정도로 매우 짧다.
L2 캐시 (Level 2 Cache):
- L1 캐시보다는 크기가 크고, 접근 속도는 약간 느리다.
- 명령어와 데이터를 함께 저장하는 통합 캐시(unified cache) 형태이다.
- 약 256KB 크기에, L1과 마찬가지로 8-way set associative 구조를 가진다.
- 접근 지연 시간은 약 11 사이클 정도이다.
L3 캐시 (Level 3 Cache):
- L2 캐시보다 훨씬 크고, 속도는 더 느리다. 여러 코어가 공유하기도 한다.
- L2와 마찬가지로 통합 캐시이며, 8MB 또는 그 이상의 크기를 가질 수 있다.
- 16-way set associative 구조로, L1/L2보다 더 높은 연결성(associativity)을 가진다. (이는 더 많은 위치에 데이터를 저장할 수 있음을 의미하며, 캐시 미스를 줄이는 데 도움이 될 수 있다.)
- 접근 지연 시간은 30-40 사이클 정도로, L1/L2에 비해 상대적으로 길지만 여전히 메인 메모리보다는 훨씬 빠르다.

여기서 중요한 점은 모든 캐시 레벨(L1, L2, L3)에서 블록 크기(캐시 라인)는 64바이트로 동일하다는 것이다. CPU는 데이터를 찾을 때 L1 캐시부터 시작해서 L2, L3, 그리고 마지막으로 메인 메모리 순으로 찾아 내려간다. 상위 레벨 캐시에서 히트할 확률을 높이는 것이 전체 시스템 성능 향상의 핵심이다.

3. 캐시 성능 측정과 영향: The Memory Mountain 🏔️

캐시의 성능은 프로그램이 메모리에 어떻게 접근하는지에 따라 크게 달라진다. 주요 성능 지표로는 다음과 같은 것들이 있다.

미스율 (Miss Rate): 전체 메모리 접근 중 캐시 미스가 발생한 비율이다. 낮을수록 좋다.
히트율 (Hit Rate): 1 - 미스율. 높을수록 좋다.
미스 패널티(Miss Penalty): 하나의 미스가 발생함으로써 추가로 드는 시간
평균 메모리 접근 시간 (Average Memory Access Time, AMAT): (히트 시간) + (미스율) × (미스 패널티)로 계산되며, 실제 프로그램이 느끼는 평균적인 메모리 접근 속도이다.
처리량 (Throughput): 단위 시간당 전송할 수 있는 데이터의 양 (예: MB/s).

AMAT calculation

"The Memory Mountain"은 이러한 캐시 성능을 직관적으로 보여주는 아주 유익한 그래프다. 이 그래프는 프로그램의 읽기 처리량(read throughput)이 두 가지 변수, 즉 작업 집합 크기(Working set size)와 스트라이드(Stride)에 따라 어떻게 변하는지를 3차원 형태로 시각화한다.

Working set size: 프로그램이 짧은 시간 동안 활발하게 접근하는 데이터 영역의 크기이다.
Stride: 연속적인 데이터 접근 시 메모리 주소 간의 간격이다. 예를 들어, 배열 a[0], a[1], a[2]를 순차적으로 접근하면 stride는 1 (데이터 요소 크기 기준)이고, a[0], a[2], a[4]를 접근하면 stride는 2이다.

Intel Core i7 Memory Mountain

주어진 Intel Core i7 시스템의 Memory Mountain 그래프를 살펴보면 다음과 같은 중요한 특징을 관찰할 수 있다.

Working set size가 작을 때 (L1 캐시 영역):
- 처리량이 매우 높게 나타난다. 이는 작업 데이터셋 전체가 L1 캐시(예: 32KB)에 완전히 들어갈 수 있을 만큼 작아서, 대부분의 접근이 L1 히트로 이어지기 때문이다. 이 영역이 가장 높은 봉우리를 형성한다.
Working set size가 점차 커질 때 (L2, L3 캐시 영역 및 메인 메모리 영역):
- 처리량이 단계적으로 뚝뚝 떨어지는 것을 볼 수 있다.
  - Working set size가 L1 캐시 크기를 넘어서면, L2 캐시를 주로 사용하게 되어 처리량이 감소한다.
  - 다시 L2 캐시 크기(예: 256KB)를 넘어서면, L3 캐시를 주로 사용하게 되어 처리량이 더 감소한다.
  - L3 캐시 크기(예: 8MB)마저 넘어서면, 이제 메인 메모리까지 접근해야 하므로 처리량은 더욱 크게 감소한다.
- 이러한 계단식 감소는 캐시 계층 구조의 성능 특성을 명확히 보여준다.
스트라이드(Stride)의 영향 - 지역성의 중요성:
- 시간 지역성의 능선 (Ridges of Temporal Locality):
  - 시간 지역성(Temporal Locality)이란 최근에 접근한 데이터는 가까운 미래에 다시 접근될 가능성이 높다는 원리이다.
  - Working set size가 특정 캐시 크기(L1, L2, L3) 내에 잘 머무는 경우 (즉, 데이터가 해당 캐시에 계속 상주할 수 있을 때), 스트라이드 값에 비교적 덜 민감하게 높은 처리량을 유지하는 경향이 있다. 그래프에서 특정 working set size 범위에 걸쳐 나타나는 '능선' 부분이 이를 대변한다. 이 능선 위에서는 데이터가 캐시에 머무르며 반복적으로 사용되므로 스트라이드가 다소 크더라도 성능이 유지된다.
- 공간 지역성의 경사면 (Slopes of Spatial Locality):
  - 공간 지역성(Spatial Locality)이란 어떤 데이터에 접근했을 때, 그 근처의 데이터가 곧 접근될 가능성이 높다는 원리이다.
  - 스트라이드 값이 작을수록 (즉, 메모리 상에서 인접한 데이터를 순차적으로 접근할수록), 캐시 라인(예: 64바이트)에 함께 로드된 주변 데이터를 효율적으로 활용할 수 있어 높은 처리량을 얻는다. 이는 마치 한 번 장 보러 갈 때 여러 물건을 한 번에 카트에 담아오는 것과 같다.
  - 반대로 스트라이드 값이 커질수록, 특히 캐시 라인 크기 이상으로 커지면, 캐시 라인에 로드된 데이터 중 극히 일부만 사용하고 나머지는 버리게 되어 공간 지역성을 제대로 활용하지 못한다. 이는 불필요한 메모리 대역폭 낭비와 캐시 미스를 유발하여 처리량을 급격히 떨어뜨린다. 그래프에서 스트라이드가 증가함에 따라 처리량이 가파르게 떨어지는 '경사면'이 이를 보여준다.

이 Memory Mountain은 캐시 크기와 메모리 접근 패턴(working set size, stride)이 시스템 성능에 얼마나 지대한 영향을 미치는지 극명하게 보여준다. 따라서, 캐시 친화적인(cache-friendly) 코드를 작성하는 것이 얼마나 중요한지 다시 한번 깨닫게 된다. 캐시 친화적인 코드란, 시간 지역성과 공간 지역성을 최대한 활용하여 캐시 히트율을 높이고 미스율을 낮추는 코드를 의미한다.

4. 예제: 행렬 곱셈(Matrix Multiplication)과 캐시 미스 분석 💻

고전적이면서도 캐시 성능에 매우 민감한 연산 중 하나가 바로 행렬 곱셈(Matrix Multiplication)이다. $N \times N$ 크기의 두 행렬 A와 B를 곱하여 행렬 C를 만드는 연산, 즉 $C = A \times B$ 는 기본적으로 $ O(n^{3})$의 시간 복잡도를 가진다.

C언어와 같은 많은 프로그래밍 언어에서 2차원 배열로 표현되는 행렬은 실제 메모리에는 행 우선 순서(row-major order)로 선형적으로 저장된다. 예를 들어 a[i][k]와 a[i][k+1]은 메모리 상에서 바로 옆에 붙어있지만 (공간 지역성 좋음), a[i][k]와 a[i+1][k]는 N개의 원소만큼 떨어져 있다 (공간 지역성 나쁨, N이 클 경우).

Reviewing C Arrays in memory

일반적인 행렬 곱셈은 3개의 중첩된 반복문(loop)을 사용하여 구현할 수 있다. 이 3개 루프의 변수 i, j, k의 순서를 어떻게 배치하느냐에 따라 총 $3! = 6$ 가지의 구현이 가능하다. 놀랍게도, 이 루프 순서에 따라 메모리 접근 패턴이 달라지고, 이는 캐시 미스율에 엄청난 차이를 만들어낸다.

여기서는 32바이트 캐시 블록 크기와 double 정밀도(8바이트)를 가정하고, 각 루프 순서별 내부 루프(inner loop) 실행 시 A, B, C 행렬 각각에 대한 대략적인 캐시 미스율을 분석해 보자. (캐시가 충분히 크지 않고, 처음 접근하는 데이터는 미스라고 가정한다.)

ijk 루프 순서:

C
for (i=0; i<n; i++) {
    for (j=0; j<n; j++) {
        sum = 0.0; // 레지스터에 저장되어 캐시 미스에 영향 없음
        for (k=0; k<n; k++) { // Inner loop
            sum += a[i][k] * b[k][j];
        }
        c[i][j] = sum;
    }
}

내부 루프 (k 루프) 에서의 접근 패턴:
- a[i][k]: k가 증가함에 따라 a[i][0], a[i][1], a[i][2], ... 순으로 접근. 이는 행 우선 접근(Row-wise access)으로, 메모리 상에서 인접한 위치에 순차적으로 접근하므로 공간 지역성이 매우 좋다. 4개의 double (32바이트)마다 한 번 미스가 발생한다고 가정하면, Misses per inner loop iteration $\approx 8/32 = 1/4 = 0.25$ .
- b[k][j]: k가 증가함에 따라 b[0][j], b[1][j], b[2][j], ... 순으로 접근. 이는 열 우선 접근(Column-wise access)이다. b[k][j]와 b[k+1][j]는 메모리 상에서 $N \times sizeof(double)$ 만큼 떨어져 있다. 캐시 라인 크기(32바이트)보다 이 간격이 크다면, 매 접근마다 새로운 캐시 라인을 가져와야 하므로 거의 매번 미스가 발생한다. Misses per inner loop iteration $\approx 1.0$ .
- c[i][j]: 내부 루프 동안 c[i][j]의 주소는 고정되어 한 번 계산된 sum을 저장하는 데만 사용된다. 보통 이 값은 레지스터에 있거나, 외부 루프에서 이미 캐시에 로드되었을 가능성이 높다. Misses per inner loop iteration $\approx 0.0$ .
총 추정 미스율 (Misses per inner loop iteration) $\approx 0.25 + 1.0 + 0.0 = 1.25$

jik 루프 순서: ijk와 마찬가지로 내부 루프는 k에 대해 돌고, a[i][k]는 행 우선, b[k][j]는 열 우선 접근이다.

총 추정 미스율 $\approx 1.25$

kij 루프 순서:

C
for (k=0; k<n; k++) {
    for (i=0; i<n; i++) {
        r = a[i][k]; // 레지스터에 저장
        for (j=0; j<n; j++) { // Inner loop
            c[i][j] += r * b[k][j];
        }
    }
}

내부 루프 (j 루프) 에서의 접근 패턴:
- a[i][k]: r에 저장되어 내부 루프에서는 반복 접근. 첫 접근 시 미스가 날 수 있지만, 내부 루프 반복 중에는 미스 없음. (또는 외부 루프에서 이미 캐싱되었다고 가정) Misses per inner loop iteration $\approx 0.0$ .
- b[k][j]: j가 증가함에 따라 b[k][0], b[k][1], b[k][2], ... 순으로 접근. 행 우선 접근. Misses per inner loop iteration $\approx 0.25$ .
- c[i][j]: j가 증가함에 따라 c[i][0], c[i][1], c[i][2], ... 순으로 접근. 행 우선 접근. Misses per inner loop iteration $\approx 0.25$ .
총 추정 미스율 $\approx 0.0 + 0.25 + 0.25 = 0.5$

ikj 루프 순서: kij와 마찬가지로 내부 루프는 j에 대해 돌고, a[i][k]는 고정, b[k][j]와 c[i][j]는 행 우선 접근이다.

총 추정 미스율 $\approx 0.5$

jki 루프 순서:

C
for (j=0; j<n; j++) {
    for (k=0; k<n; k++) {
        r = b[k][j]; // 레지스터에 저장
        for (i=0; i<n; i++) { // Inner loop
            c[i][j] += a[i][k] * r;
        }
    }
}

내부 루프 (i 루프) 에서의 접근 패턴:
- a[i][k]: i가 증가함에 따라 a[0][k], a[1][k], a[2][k], ... 순으로 접근. 열 우선 접근. Misses per inner loop iteration $\approx 1.0$ .
- b[k][j]: r에 저장되어 내부 루프에서는 반복 접근. Misses per inner loop iteration $\approx 0.0$ .
- c[i][j]: i가 증가함에 따라 c[0][j], c[1][j], c[2][j], ... 순으로 접근. 열 우선 접근. Misses per inner loop iteration $\approx 1.0$ .
총 추정 미스율 $\approx 1.0 + 0.0 + 1.0 = 2.0$

kji 루프 순서: jki와 마찬가지로 내부 루프는 i에 대해 돌고, a[i][k]와 c[i][j]는 열 우선 접근, b[k][j]는 고정이다.

총 추정 미스율 $\approx 2.0$

결론 및 실제 성능과의 비교:

이 추정 미스율을 보면, kij와 ikj 루프 순서가 0.5로 가장 낮고, ijk와 jik 순서가 1.25, 그리고 jki와 kji 순서가 2.0으로 가장 높게 나타난다. 이는 실제 Core i7과 같은 현대 프로세서에서 측정한 성능 그래프와 매우 유사한 경향을 보인다! 성능 그래프에서 내부 루프 반복 당 사이클 수(cycles per inner loop iteration)가 낮을수록 성능이 좋은 것인데, kij/ikj 그룹이 가장 낮은 사이클 수를 보여 가장 빠르고, ijk/jik 그룹이 중간, jki/kji 그룹이 가장 높은 사이클 수를 보여 가장 느리다.

Core i7 matrix Multiply Performance

이 분석은 단순히 루프의 순서를 바꾸는 것만으로도 메모리 접근 패턴이 크게 달라지고, 이로 인해 캐시 미스율이 변하여 최종 프로그램 성능에 막대한 영향을 미친다는 것을 극명하게 보여준다. kij와 ikj가 좋은 성능을 보이는 이유는 내부 루프에서 접근하는 두 개의 큰 배열(b와 c)이 모두 행 우선으로 접근되어 공간 지역성을 최대한 활용하기 때문이다. 반대로 jki와 kji는 내부 루프에서 접근하는 두 배열(a와 c)이 모두 열 우선으로 접근되어 공간 지역성이 최악이므로 성능이 가장 나쁘다.

더 나아가: 블록 행렬 곱셈 (Blocked Matrix Multiplication)

대규모 행렬 곱셈에서는 단순히 루프 순서를 변경하는 것만으로는 캐시의 용량 한계(capacity miss)를 극복하기 어렵다. Working set size가 L3 캐시 크기마저 넘어서면, 아무리 접근 순서를 최적화해도 결국 많은 데이터가 캐시에 담기지 못하고 미스가 발생하기 때문이다.

이를 개선하기 위한 강력한 기법이 바로 블록 행렬 곱셈(Blocked Matrix Multiplication) 또는 타일링(Tiling)이라고 불리는 기법이다. 이는 큰 행렬을 여러 개의 작은 블록(sub-matrices)으로 나누어, 각 블록 단위의 연산을 수행할 때 필요한 데이터(A, B, C 행렬의 해당 블록들)가 상위 레벨 캐시(예: L1 또는 L2)에 최대한 머무르도록 하는 방법이다.

Blocked Matrix Multiplication

적절한 블록 크기 B를 선택하면, 내부의 3중 루프가 B×B 크기의 서브 행렬들을 처리하는 동안 이 데이터들이 캐시에 계속 상주(temporal locality)하면서 연산이 이루어지도록 할 수 있다. 이렇게 하면 캐시 미스 발생을 극적으로 줄일 수 있다. 이때 블록 크기는 L1 캐시 크기 등을 고려하여 3 * B^2 * sizeof(double) < L1_cache_size 와 같은 조건을 만족하도록 신중하게 선택해야 한다.

5. 결론: 캐시, 성능 최적화의 숨은 조력자

시스템 프로그래밍의 세계에서 캐시의 동작 원리와 그 성능에 대한 깊이 있는 이해는 아무리 강조해도 지나치지 않다. 메모리는 단순히 데이터를 저장하는 수동적인 공간이 아니라, 복잡한 계층 구조와 캐싱 메커니즘을 통해 시스템 전체 성능에 결정적인 영향을 미치는 능동적인 자원임을 오늘 다시 한번 확인했다.

이번 학습을 통해 우리는 다음을 명확히 이해할 수 있었다.

캐시는 메인 메모리 블록의 부분 집합을 저장하여 CPU의 데이터 접근 지연 시간을 줄인다.
캐시 히트와 캐시 미스의 개념은 캐시 성능 평가의 기본이다.
Intel Core i7과 같은 현대 CPU는 L1, L2, L3와 같은 다단계 캐시 계층 구조를 가진다.
Memory Mountain 분석은 Working set size와 Stride가 캐시 성능, 특히 공간 지역성과 시간 지역성 활용에 어떻게 영향을 미치는지 정량적으로 보여주었다.
행렬 곱셈 예제는 동일한 연산이라도 코드의 메모리 접근 패턴(루프 순서)에 따라 캐시 미스율이 극적으로 달라지며, 이것이 실제 성능 차이로 이어진다는 것을 실증적으로 보여주었다. 캐시 친화적인 코드 작성의 중요성은 아무리 강조해도 부족하다!

결국, 고성능 시스템을 설계하고 구현하기 위해서는 이러한 low-level에서의 메모리 동작을 세심하게 고려한 프로그래밍과 알고리즘 설계가 필수적이다. 캐시 미스를 줄이는 것은 CPU가 불필요하게 기다리는 시간을 최소화하고, 실제 유용한 연산에 더 많은 시간을 할애할 수 있도록 하는 핵심 과제임을 명심해야겠다.