이전 글들에서 공간/주파수 영역 필터링과 이미지 분할 기법들을 살펴보았다. 이번에는 이미지 내 객체의 형태(Shape)와 구조(Structure)를 직접 다루는 또 다른 강력한 이미지 처리 도구인 형태학적 필터(Morphological Filter)에 대해 학습한 내용을 정리해보고자 한다.
1. 형태학적 필터란?
형태학적 필터(Morphological Filter)는 이미지 처리(Image Processing) 분야에서 이미지 내 객체의 형태와 구조를 분석하고 처리하는 데 사용되는 비선형(non-linear) 필터 기법이다. 생물학에서 형태학이 유기체의 형태와 구조를 연구하는 것처럼, 영상 처리에서의 형태학은 이미지 속 영역(객체)의 모양, 경계, 뼈대(skeleton) 등을 기술하고 분석하는 데 중점을 둔다.
형태학적 필터는 주로 이진(binary) 이미지를 대상으로 적용되며, 이미지 내 객체의 형태를 구조 요소(Structuring Element)라고 불리는 작은 패턴과의 상호작용을 통해 변형시킨다. 이러한 형태 변환을 통해 노이즈 제거, 객체 분리, 특징 추출 등 다양한 영상 처리 목표를 달성할 수 있다. 근본적으로 형태학적 연산은 이미지의 전경(Foreground) 픽셀 집합과 배경(Background) 픽셀 집합 간의 관계를 구조 요소를 이용하여 탐색하고 조작하는 과정이다.
2. 기본적인 형태학적 연산
형태학적 필터의 가장 기본이 되는 두 가지 연산은 팽창(Dilation)과 침식(Erosion)이다.
2.1 팽창 (Dilation)
팽창(Dilation) 연산은 이미지의 전경 영역을 말 그대로 "팽창"시키거나 내부의 작은 구멍을 채우는(fill) 효과를 가진다. 확장(expand) 또는 성장(grow) 연산이라고도 불린다. 팽창 연산의 핵심은 구조 요소(Structuring Element)와의 관계에 있다.
- 팽창 연산은 특정 형태를 가진 구조 요소(커널)를 사용하여 수행된다.
- 이미지 내 특정 픽셀 위치에 구조 요소의 기준점(origin)을 놓았을 때, 구조 요소가 덮는 영역 내에 적어도 하나의 전경 픽셀이 존재한다면, 해당 기준점 위치의 출력 이미지 픽셀은 전경 픽셀이 된다.
- 즉, 구조 요소가 이미지의 전경 영역 위를 이동하면서, 구조 요소에 조금이라도 닿는 주변 배경 픽셀들을 전경 픽셀로 확장시키는 효과를 낸다.
- 따라서, 사용하는 구조 요소의 크기가 클수록 더 넓은 영역이 팽창되며, 구조 요소의 형태(예: 사각형, 원형, 선형)에 따라 팽창되는 방향이나 모양이 달라질 수 있다.
- 특히, 구조 요소의 크기보다 작은 전경 객체 내부의 구멍(hole)을 메우는 데 유용하게 사용된다.
 |
| Dilation |
2.2 침식 (Erosion)
침식(Erosion) 연산은 이미지의 전경 영역을 "침식"시켜 축소하거나 제거하는(remove) 효과를 가진다. 수축(shrink) 또는 감소(reduce) 연산이라고도 한다. 침식 연산 역시 구조 요소와 밀접한 관련이 있다.
- 침식 연산 또한 특정 형태의 구조 요소(커널)를 사용하여 수행된다.
- 이미지 내 특정 픽셀 위치에 구조 요소의 기준점을 놓았을 때, 구조 요소가 덮는 영역 내의 모든 픽셀이 원본 이미지에서도 전경 픽셀이어야만, 해당 기준점 위치의 출력 이미지 픽셀이 전경 픽셀로 유지된다. 만약 구조 요소 내에 하나라도 배경 픽셀에 해당하는 위치가 있다면, 출력 픽셀은 배경 픽셀이 된다.
- 즉, 구조 요소가 이미지의 전경 영역 위를 이동하면서, 구조 요소가 완전히 들어맞지 않는 경계 부분의 전경 픽셀들을 제거(배경으로 만듦)하는 효과를 낸다.
- 따라서, 구조 요소의 크기가 클수록 더 많은 영역이 침식되어 사라지며, 구조 요소의 형태에 따라 침식되는 모양이 달라진다.
- 주로 구조 요소의 크기보다 작은 노이즈(예: 작은 흰 점)나 가는 연결선 등을 제거하는 데 유용하게 사용된다.
 |
| Erosion |
3. 복합적인 형태학적 연산
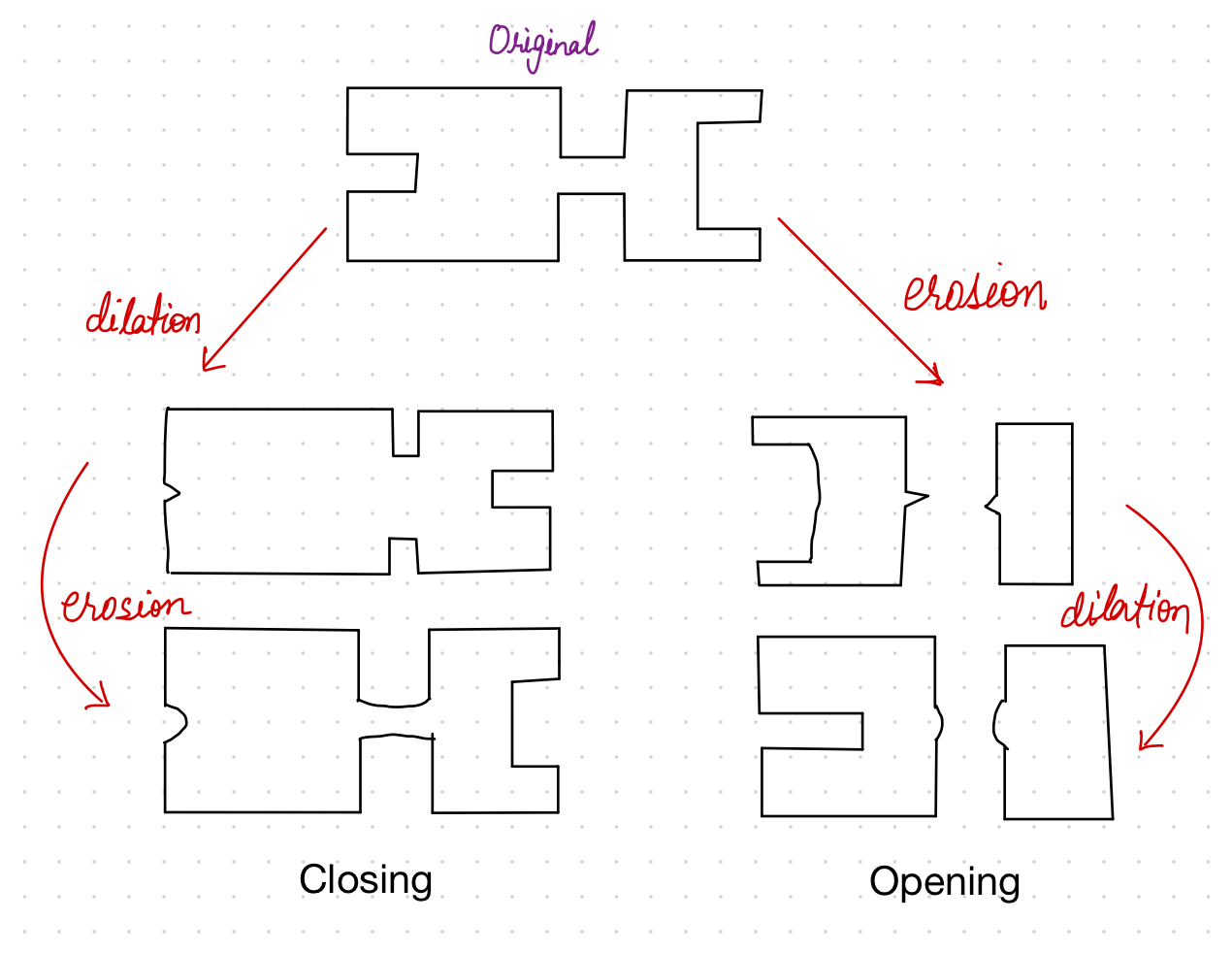
기본적인 팽창과 침식 연산을 특정 순서로 조합하여 더 복잡하고 유용한 형태학적 연산을 만들 수 있다. 대표적인 예가 열기(Opening)와 닫기(Closing) 연산이다.
3.1 열기 (Opening)
열기(Opening) 연산은 이미지에 대해 침식(Erosion)을 먼저 수행한 후, 그 결과에 동일한 구조 요소를 사용하여 팽창(Dilation)을 수행하는 연산이다. 이러한 '침식 후 팽창' 순서 때문에 다음과 같은 효과를 가진다.
- 객체의 전체적인 크기는 유지하면서 윤곽을 부드럽게 만든다.
- 객체들 사이를 잇는 좁은 연결 부위(다리)를 끊는다.
- 구조 요소보다 작은 크기의 돌출부나 고립된 작은 점(노이즈)들을 제거한다.
열기 연산은 주로 다음과 같은 종류의 노이즈 제거에 효과적이다.
- 작은 크기의 밝은 노이즈 (small bright noise): 침식 단계에서 제거된다.
- 가늘고 뾰족한 돌출부 (thin protrusions or sharp peaks): 침식으로 제거된 후 팽창해도 복원되지 않아 부드러워진다.
 |
| example |
3.2 닫기 (Closing)
닫기(Closing) 연산은 열기와 반대 순서로, 이미지에 대해 팽창(Dilation)을 먼저 수행한 후, 그 결과에 동일한 구조 요소를 사용하여 침식(Erosion)을 수행하는 연산이다. 이러한 '팽창 후 침식' 순서로 인해 다음과 같은 효과를 나타낸다.
- 객체의 전체적인 크기는 유지하면서 윤곽을 부드럽게 만든다.
- 객체 내부의 작은 구멍이나 틈을 메운다.
- 객체 윤곽의 좁은 끊김이나 만(gulf) 형태를 연결한다.
닫기 연산은 주로 다음과 같은 종류의 결함을 보완하는 데 유용하다.
- 객체 내부 또는 윤곽선의 작은 구멍 (small holes)
- 좁게 끊어진 부분 (narrow breaks)
- 객체 경계의 깊고 좁은 만 (long thin gulfs)
 |
| example |
opening과 closing의 효과를 잘 보여주는 이미지를 통해 다시 살펴보자.
 |
| closing vs opening |
4. 세선화 (Thinning)
세선화(Thinning)는 객체의 폭을 한 픽셀 두께로 줄여서 객체의 뼈대(Skeleton) 또는 중심선을 추출하는 형태학적 연산이다. 이는 다음과 같은 이미지 분석 분야에서 유용하게 활용될 수 있다.
- 골격화(Skeletonization): 객체의 위상(topology) 정보는 유지하면서 두께를 줄여 형태 분석, 특징 추출, 객체 매칭 등에 활용한다. 예를 들어, 손글씨 문자 인식이나 지문 인식 등에서 문자의 획이나 지문의 융선을 표현하는 데 핵심적인 역할을 수행한다.
- 윤곽선 정리: 엣지 검출기(edge detector)로 얻은 두꺼운 윤곽선 결과물을 한 픽셀 두께로 정리하여 더 명확한 경계 정보를 얻는 데 도움을 준다.
- 선과 코너 특징 추출: 이미지를 한 픽셀 두께의 선으로 표현하면 선의 분기점이나 코너의 위치를 명확하게 파악할 수 있어, 이러한 특징 기반의 객체 인식에 유용하다.
세선화 연산의 구체적인 동작 방식은 사용하는 구조 요소에 의해 결정되며, 주로 Hit-or-Miss Transform에 사용되는 특수한 형태의 구조 요소들을 활용하여 객체의 경계 픽셀들을 객체의 연결성을 유지하면서 반복적으로 제거하는 방식으로 이루어진다. 이때, 선의 끝점(endpoint)은 일반적으로 보존된다.
 |
| Thinning Process |
5. 결론
형태학적 필터는 구조 요소와의 상호작용을 통해 이미지 내 객체의 형태와 구조를 효과적으로 분석하고 변형할 수 있는 강력한 이미지 처리 도구이다. 기본적인 팽창과 침식 연산부터 이를 조합한 열기, 닫기, 그리고 객체의 뼈대를 추출하는 세선화까지, 다양한 연산을 통해 노이즈 제거, 특징 추출, 객체 분리 등 다양한 컴퓨터 비전 문제 해결에 기여한다. 특히 이진 이미지 처리에서 그 효과가 두드러지며, 다양한 응용 분야에서 핵심적인 전처리 또는 분석 기법으로 사용된다.
추천글:
[컴퓨터비전개론] Fourier Transform - Filtering in Frequency Domain (Low Pass Filter, High Pass Filter)
[컴퓨터비전개론] Image Segmentation - Active Contour, Region Growing
