[컴퓨터비전개론] Object Recognition - Decision-theoretic methods, Minimum distance classifier

이번 학기 컴퓨터 비전 중간고사 범위 학습의 마지막 주제로 객체 인식(Object Recognition)의 기본 원리에 대해 정리한다. 이미지 필터링, 분할, 형태학적 분석 등 이전 단계들을 거쳐, 이제 이미지 내에 '무엇'이 있는지를 컴퓨터가 식별하고 분류하는 핵심 과제를 다룬다. 객체 인식은 컴퓨터 비전(Computer Vision)의 궁극적인 목표 중 하나이며, 자율 주행, 의료 영상 분석, 로봇 공학, 보안 시스템 등 다양한 응용의 기반이 되는 필수 기술이다.

1. 객체 인식의 기본 개념 및 중요성

객체 인식은 주어진 입력 패턴(예: 이미지의 특정 영역)이 사전에 정의된 여러 클래스 중 어느 클래스에 속하는지를 판별하는 과정이다. 여기서 패턴(Pattern)은 객체를 설명하는 여러 Descriptor들의 배열로 정의될 수 있으며, 특징(Feature)이 Descriptor에 대응되는 개념이다. 유사한 속성(특징)을 공유하는 패턴들의 집합은 하나의 패턴 클래스(Pattern Class)를 형성한다.

객체 인식의 정확도는 컴퓨터를 이용한 분석 절차 전체의 성공 여부를 결정짓는 매우 중요한 요소이다. 많은 경우 객체 인식을 수행하기 전에 이미지 분할(Image Segmentation) 과정을 통해 관심 객체 영역을 먼저 추출하지만, 분할과 인식이 동시에 또는 거의 동시에 이루어지기도 한다.

2. 패턴 표현 방식

객체를 인식하기 위해서는 먼저 객체의 특징을 효과적으로 표현(representation)해야 한다. 이는 객체 인식 시스템의 성능에 결정적인 영향을 미친다. 일반적인 패턴 표현 방식은 다음과 같다.

벡터 표현(Vector Description): 객체의 정량적인 속성(측정값)들을 순서대로 나열한 벡터 형태로 표현하는 방식이다. 벡터의 각 성분은 하나의 기술자(descriptor) 또는 특징(feature)을 나타내며, 벡터의 차원은 사용된 기술자의 총 수를 의미한다. 예를 들어, 꽃 이미지에서 꽃잎의 평균 길이와 평균 너비를 측정하여 [길이, 너비] 와 같은 2차원 패턴 벡터로 표현할 수 있다.

문자열 표현(String Description): 객체의 경계(boundary) 형태와 관련된 기본적인 구조 요소들의 연결 순서를 기반으로 문자열 형태로 표현하는 방식이다. 주로 단순한 연결 구조를 가진 객체의 형태를 표현하는 데 적합하다.

트리 표현(Tree Description): 객체를 구성하는 요소들 간의 계층적인 구조적 관계를 트리(tree) 형태로 표현하는 방식이다. 복잡한 구조를 가진 객체의 특징을 나타내는 데 유용하며, 예를 들어 지문 인식에서 융선의 분기점이나 끝점과 같은 특징점들 간의 상호 관계를 기술하는 데 활용될 수 있다.

3. 결정 이론적 방법(Decision-Theoretic Methods)

결정 이론적 접근 방식은 패턴 인식(Pattern Recognition) 문제에 통계적 결정 이론을 적용하는 방법이다. 이 방식은 각 클래스마다 판별 함수(Discriminant Function)를 정의하여, 입력 패턴을 특정 클래스에 할당(분류)한다.

만약 총 W개의 클래스가 존재한다면, 각 클래스 $w_{i} $( $i = 1, 2, ..., W$ )에 대한 판별 함수 $d_{i}(x) $를 정의한다. 이 판별 함수는 입력 패턴 x가 클래스 w_i에 속할 때 다른 모든 클래스 w_j ( $j \neq i$ )에 대한 판별 함수 값보다 더 큰 값을 갖도록 설계된다 ( $$d_{i}(x) $ >$ $d_{j}(x) $). 따라서, 알 수 없는 새로운 패턴 x가 입력되었을 때, 모든 판별 함수 $d_{1}(x) $,$d_{2}(x) $,...,$d_{W}(x) $를 계산하여 가장 큰 값을 산출하는 클래스로 x를 분류한다.

3.1 최소 거리 분류기(Minimum Distance Classifier, MDC)

최소 거리 분류기(Minimum Distance Classifier, MDC)는 결정 이론적 방법 중 가장 간단하고 직관적인 분류기 중 하나이다. 이 방법은 각 클래스를 대표하는 원형 벡터(Prototype Vector)를 설정하고, 입력 패턴 벡터와 각 클래스의 원형 벡터 사이의 거리를 계산하여 가장 가까운(거리가 최소인) 클래스로 분류한다.

일반적으로 각 클래스의 원형 벡터는 해당 클래스에 속하는 모든 학습 패턴 벡터들의 평균 벡터(Mean Vector)로 정의된다. 입력 패턴 x를 클래스 w_i로 분류하는 조건은 x와 w_i의 원형 벡터(평균 벡터) 사이의 유클리드 거리(Euclidean distance) D_i(x)가 다른 모든 클래스 w_j에 대한 거리 D_j(x)보다 작을 때이다 ( $D_{i} (x) < D_{j} (x) \forall j\neq i$ ). 이는 가장 작은 거리가 가장 높은 유사도(가장 큰 판별 함수 값)를 의미한다고 간주하기 때문이다.

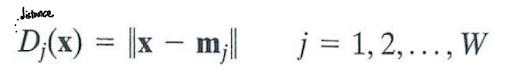formula

최소 거리 분류기는 클래스들의 평균 벡터 간 거리가 각 클래스 내 패턴들의 분산(퍼짐 정도)에 비해 상대적으로 클 경우 효과적으로 작동한다. 즉, 각 클래스의 패턴들이 해당 클래스의 평균 벡터를 중심으로 비교적 좁게 모여 있고, 클래스 간의 평균 벡터가 서로 멀리 떨어져 있을 때 좋은 성능을 보인다. 이상적으로는 각 클래스의 분포가 평균을 중심으로 하는 구형(spherical) 형태의 "초구름(hypercloud)"을 이룰 때 최적의 성능을 보인다.

Iris example

4. 특징 추출(Feature Extraction)

어떤 특징(Feature)을 추출하여 객체 인식 시스템에 사용하느냐는 시스템의 성능을 결정하는 매우 중요한 요소이다. 좋은 특징은 같은 클래스에 속하는 패턴들 사이의 변동(intra-class variation)에는 덜 민감하면서도, 서로 다른 클래스에 속하는 패턴들 간의 차이(inter-class variation)는 잘 구별해주어야 한다.

예를 들어, 의료 영상에서 종양과 혈관을 구별하기 위한 특징 추출의 예로 다음을 들 수 있다.

영역(Area): 객체가 차지하는 총 픽셀 수.
원형도(Circularity): 객체의 형태가 원에 얼마나 가까운지를 나타내는 지표. (계산식: 원형도 = $4 π \times \frac{영역}{( 둘레 ) ^{2}}$ , 원에 가까울수록 1에 근접).
경계와의 근접성(Nearness to Boundary): 객체가 이미지의 경계로부터 얼마나 가까이 위치하는지를 나타내는 거리.

실제 의료 영상 분석 사례에서 종양과 혈관은 영역, 원형도, 경계 근접성 등의 특징 값에서 평균과 표준 편차가 뚜렷하게 다른 경향을 보인다. 이러한 통계적 차이를 이용하여 최소 거리 분류기와 같은 방법을 통해 두 유형의 객체를 식별할 수 있다.

Distinguishing tumors from blood vessels

5. 최소 거리 분류기의 한계점

최소 거리 분류기는 개념이 간단하고 구현이 용이하다는 장점이 있지만, 다음과 같은 상황에서는 분류 성능이 저하될 수 있다.

클래스 간 평균 벡터 거리가 가깝고 클래스 내 패턴들의 분산이 큰 경우 (클래스들이 서로 많이 겹치는 경우).
클래스의 실제 분포가 평균 벡터 중심의 구형이 아닌 길쭉하거나 복잡한 형태를 띠는 경우.
분류에 사용해야 할 특징의 수(벡터의 차원)가 너무 많아지는 경우 (차원의 저주, Curse of Dimensionality).

6. 결론

객체 인식은 컴퓨터 비전의 핵심 연구 분야로서, 다양한 패턴 표현 방식과 결정 이론적 방법들을 통해 발전해왔다. 인식 대상 객체의 특성을 잘 반영하는 효과적인 특징 추출과 문제 상황에 적합한 분류기(classifier)를 선택하는 것은 객체 인식 시스템의 성능을 극대화하는 데 필수적이다. 최소 거리 분류기와 같은 전통적인 방법론은 특정 조건 하에서는 명확한 한계를 가질 수 있다. 최근에는 딥러닝(Deep Learning) 기술에 기반한 객체 인식 방법들이 훨씬 더 복잡한 문제에서 강력한 성능을 보여주고 있다. 하지만 객체의 기본적인 특징을 이해하고 이를 바탕으로 패턴을 분류하는 기본적인 원리는 여전히 중요하며, 앞으로도 다양한 분야에서 객체 인식 기술의 발전과 응용이 더욱 활발해질 것으로 기대된다.

[컴퓨터비전개론] Image Segmentation - Active Contour, Region Growing

[컴퓨터비전개론] Mophological Filter - Dilation, Erosion, Opening, Closing, Thinning