스플레이 트리 (Splay Tree)
지난 포스팅에서는 Balanced Search Tree의 대표적인 예시인 AVL 트리에 대해 알아보았다. 오늘은 Balanced Search Tree에 근사하는 스플레이 트리(Splay Tree)에 대해 자세히 알아보겠다. 스플레이 트리는 접근 지역성(Locality of Reference)을 활용하여 최근 접근한 노드를 루트 노드에 가깝게 위치시키는 특징을 갖고 있다.
1. 스플레이 트리란?
스플레이 트리는 이진 탐색 트리의 일종으로, 노드 접근 시마다 스플레이(splay) 연산을 수행하여 트리의 구조를 변경한다. 스플레이 연산은 접근한 노드를 루트 노드까지 올리는 과정으로, 이를 통해 자주 접근하는 노드가 루트 노드에 가깝게 위치하게 되어 탐색 시간을 단축할 수 있다.
2. 스플레이 트리의 핵심 원리
스플레이 트리의 핵심 원리는 접근 지역성(Locality of Reference)다. 접근 지역성은 최근에 접근한 데이터에 다시 접근할 확률이 높다는 특징을 의미한다. 스플레이 트리는 이러한 접근 지역성을 활용하여 자주 접근하는 노드를 루트 노드에 가깝게 위치함으로써 탐색, 삽입, 삭제 연산의 효율성을 높인다.
3. 스플레이 연산 (Splaying Operation)
스플레이 연산은 접근한 노드를 루트 노드까지 올리는 과정으로, 다음과 같은 세 가지 경우로 나누어 수행된다.
- Zig: 접근한 노드가 루트 노드의 자식인 경우, 한 번의 회전(rotation)을 통해 접근한 노드를 루트 노드로 만든다.
- Zig-Zig: 접근한 노드와 부모 노드가 모두 왼쪽 또는 오른쪽 자식인 경우, 두 번의 회전을 통해 접근한 노드를 루트 노드로 만든다.
- Zig-Zag: 접근한 노드가 부모 노드의 왼쪽 자식이고 부모 노드가 루트 노드의 오른쪽 자식인 경우 (또는 그 반대의 경우), 두 번의 회전을 통해 접근한 노드를 루트 노드로 만든다.
 |
| Splaying operation |
4. 스플레이 트리의 탐색, 삽입, 삭제
- 탐색 (Search): 이진 탐색 트리와 동일하게 탐색을 수행한 후, 찾은 노드 또는 탐색이 종료된 외부 노드(external node)에 대해 스플레이 연산을 수행한다.
- 삽입 (Insertion): 이진 탐색 트리와 동일하게 삽입을 수행한 후, 새로 생성된 노드에 대해 스플레이 연산을 수행한다.(새 노드가 root에)
 |
| splay tree insertion |
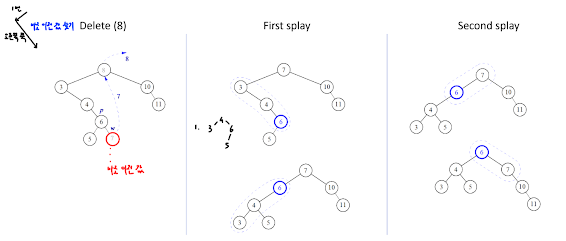
- 삭제 (Deletion): 이진 탐색 트리와 동일하게 삭제를 수행한 후, 실제로 삭제된 노드의 부모 노드에 대해 스플레이 연산을 수행한다.(삭제된 노드의 parent 노드가 root에)
 |
| splay tree deletion |
5. 스플레이 트리의 성능 분석
스플레이 트리의 각 연산은 최악의 경우 O(n) 시간이 걸릴 수 있다. 하지만, amortized analysis를 통해 스플레이 트리의 연산은 평균적으로 O(log n) 시간에 수행됨을 알 수 있다. (자세한 분석은 생략)
마무리하며
이번 포스팅에서는 스플레이 트리의 개념, 스플레이 연산, 그리고 탐색, 삽입, 삭제 과정에 대해 알아보았다. 스플레이 트리는 접근 지역성을 활용하여 자주 접근하는 데이터에 대한 빠른 접근을 가능하게 하는 효율적인 자료구조이다. 다음 포스팅에서는 Multiway Search Tree의 한 종류인 2-4 트리(2-4 Tree)에 대해 알아보겠다. 2-4 트리는 각 노드가 2개, 3개, 또는 4개의 자식을 가질 수 있는 특징을 가지고 있으며, balanced search tree의 또 다른 예시다.
추천글 :
(https://hyeonb.blogspot.com/2024/05/binary-search-tree_20.html)
