[자료구조] (2-4) 트리

(2, 4) 트리: balanced multi-way search tree

이전 포스팅에서 스플레이 트리에 대해 알아보았다. 이번에는 AVL 트리에 이어 또 다른 balanced search 트리인 (2, 4) 트리에 대해 자세히 알아보겠다. (2, 4) 트리는 각 노드가 최대 4개의 자식을 가질 수 있는 multi-way search 트리로, 삽입, 삭제 연산 후에도 트리의 깊이가 균형을 이루도록 하는 특징이 있다.

1. (2, 4) 트리란?

(2, 4) 트리는 다음과 같은 특징을 가진 multi-way search tree다.

노드 크기 속성(Node-Size Property): 각 내부 노드는 최대 4개의 자식을 갖는다. (즉, 2-노드, 3-노드, 4-노드가 존재)
깊이 속성(Depth Property): 모든 외부 노드는 같은 깊이를 갖는다.

이러한 특징 덕분에 (2, 4) 트리는 삽입, 삭제 연산 후에도 트리의 높이가 항상 O(log n)을 유지하며, 탐색, 삽입, 삭제 연산의 시간 복잡도를 O(log n)으로 보장한다.

2. (2, 4) 트리의 삽입 (Insertion)

(2, 4) 트리에 새로운 항목을 삽입하는 과정은 다음과 같다.

탐색: 먼저 삽입할 키 값을 검색하여 삽입할 위치의 부모 노드를 찾는다.
삽입: 해당 부모 노드에 새로운 항목을 추가한다.

inserting 30 -> overflow(노드 크기 초과)
오버플로 처리: 만약 삽입 후 노드에 5개의 자식이 생긴다면 (즉, 오버플로가 발생하면), 해당 노드를 분할(split)합니다. 분할은 다음과 같이 진행된다.

overflow handling
- 5-노드를 두 개의 노드(3-노드와 2-노드)로 분할한다.
- 3-노드는 원래 5-노드의 첫 세 자식과 첫 두 키 값을 갖는다.
- 2-노드는 원래 5-노드의 마지막 두 자식과 마지막 키 값을 갖는다.
- 원래 5-노드의 세 번째 키 값은 부모 노드로 올라간다. 이때, 부모 노드에서도 오버플로가 발생할 수 있으며, 이 경우 부모 노드를 다시 분할해야 한다.

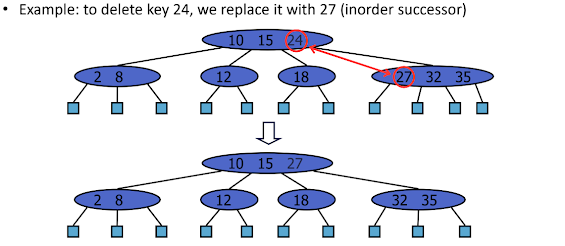
3. (2, 4) 트리의 삭제 (Deletion)

(2, 4) 트리에서 항목을 삭제하는 과정은 다음과 같다.

탐색: 먼저 삭제할 키 값을 검색하여 삭제할 노드를 찾는다.
삭제:
- 삭제할 노드가 리프 노드인 경우, 해당 노드를 삭제한다.
- 삭제할 노드가 리프 노드가 아닌 경우, inorder successor(또는 inorder predecessor)로 대체하고 inorder successor(또는 inorder predecessor)를 삭제한다.
  
  deleting 24
언더플로 처리: 만약 삭제 후 노드에 자식이 하나도 없다면 (즉, 언더플로가 발생하면), 다음 두 가지 경우 중 하나를 수행한다.
- 융합(Fusion): 인접한 형제 노드가 2-노드인 경우, 삭제된 노드와 형제 노드를 합치고 부모 노드에서 키 값 하나를 가져온다.
  
  2-node : fusion
- 이전(Transfer): 인접한 형제 노드가 3-노드 또는 4-노드인 경우, 형제 노드에서 자식 하나와 키 값 하나를 가져오고, 부모 노드의 키 값을 형제 노드로 옮긴다.
  
  3,4-node : transfer

4. (2, 4) 트리의 성능 분석

(2, 4) 트리는 삽입, 삭제 연산 시 오버플로 또는 언더플로를 처리해야 하지만, 탐색, 삽입, 삭제 연산의 시간 복잡도가 모두 O(log n)으로 보장된다. 따라서 데이터의 삽입 및 삭제가 빈번하게 발생하는 동적 데이터 환경에서 효율적인 자료구조다.

마무리하며

이번 포스팅에서는 (2, 4) tree의 개념, 삽입, 삭제 과정, 그리고 성능에 대해 알아보았다. (2, 4) tree는 balanced multi-way search tree의 대표적인 예로, 균형을 유지하면서도 효율적인 연산을 지원다. 다음 포스팅에서는 (2, 4) tree를 응용한 Red-black tree에 대해 알아보겠다.

추천글 :
[자료구조] Splay tree

(https://hyeonb.blogspot.com/2024/05/splay-tree.html)

[자료구조] AVL tree
(https://hyeonb.blogspot.com/2024/05/avl-tree.html)

[자료구조] Binary search tree
(https://hyeonb.blogspot.com/2024/05/binary-search-tree_20.html)