다익스트라 알고리즘: 가중치 그래프에서 최단 경로 찾기
가중치 그래프와 최단 경로
이전 포스팅에서는 가중치가 없는 그래프에서 최단 경로를 찾는 BFS 알고리즘에 대해 알아보았다. 그러나 실제 지도와 같이 간선에 가중치가 있는 경우 BFS는 적용할 수 없다. 가중치 그래프에서 최단 경로는 단순히 거쳐 가는 정점의 수가 가장 적은 경로가 아니라, 간선의 가중치 합이 최소가 되는 경로이다.
예를 들어, 다음과 같은 가중치 그래프를 생각해 보자.
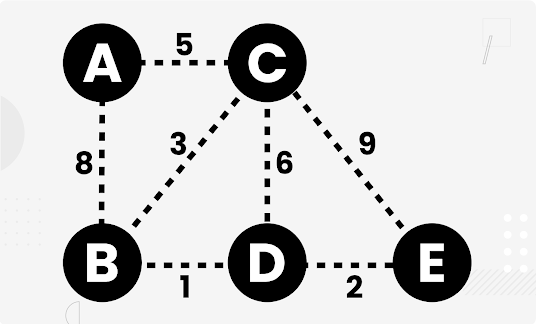 |
| weighted graph |
BFS를 사용하면 정점 A에서 정점 E까지의 최단 경로는 A-C-E가 된다. 그러나 가중치를 고려하면 A-B-D-E가 최단 경로이다.
다익스트라 알고리즘과 벨만-포드 알고리즘
가중치 그래프에서 최단 경로를 찾는 알고리즘으로는 다익스트라 알고리즘과 벨만-포드 알고리즘이 있다. 다익스트라 알고리즘은 모든 간선의 가중치가 음수가 아닌 경우에 사용할 수 있는 알고리즘이고, 벨만-포드 알고리즘은 음수 가중치를 갖는 간선이 있는 경우에도 사용할 수 있는 알고리즘이다. (여기서는 다익스트라 알고리즘에 대해서만 상세히 다뤄보도록하겠다.)
최단 경로의 부분 경로
다익스트라 알고리즘을 이해하기 위해서는 먼저 다음의 논리를 알아야 한다. 바로 최단 경로의 부분 경로 또한 최단 경로가 되어야 한다는 점이다. 예를 들어, 앞선 그림에서 A에서 E까지의 최단 경로는 A-B-D-E였다. 이때 A에서 D까지의 부분 경로는 A-B-D가 되어야 한다. 만약 A에서 D까지의 더 짧은 경로가 존재한다면, A에서 E까지의 최단 경로는 A-B-D-E가 아니라 더 짧은 경로를 포함하는 경로가 될 것이다.
다익스트라 알고리즘의 직관적인 설명
다익스트라 알고리즘은 최단 경로의 부분 경로를 하나씩 찾아나가는 방식으로 작동한다. 시작 정점에서부터 최단 경로를 찾은 정점들을 순서대로 추가해 나가면서, 마치 나무가 자라나는 것처럼 트리 구조를 형성한다. 당장 눈앞의 최단 경로를 찾아간다는 점에서 Greedy algorithm에 속하는데, 이에 대한 자세한 내용은 다음에 다뤄보도록 하겠다.
 |
| seems to be a tree |
다익스트라 알고리즘의 의사 코드
Dijkstra(G, s):
Set all vertices to not-sure
d[v] = ∞ for all v in V
d[s] = 0
while there are not-sure nodes:
Pick the not-sure node u with the smallest estimate d[u].
For v in u.neighbors:
d[v] = min(d[v], d[u]+edgeWeight(u, v))
Mark u as sure
Now d(s, v) = d[v]여기서 d[v]는 시작 정점 s에서 정점 v까지의 최단 경로의 길이를 나타낸다.
이제 의사코드를 하나씩 뜯어보자. 다익스트라 알고리즘은 다음과 같은 단계로 작동한다.
- 모든 정점에 대해 시작 정점으로부터의 거리를 무한대로 초기화한다. 시작 정점의 거리는 0으로 설정한다.
- 모든 정점을 "미확정" 상태로 표시한다.
- 미확정 정점 중에서 시작 정점으로부터의 거리가 가장 짧은 정점을 선택한다.
- 선택한 정점을 "확정" 상태로 표시한다.
- 확정된 정점의 모든 인접 정점에 대해, 현재 경로를 통한 거리가 기존 거리보다 짧으면 거리를 업데이트한다.
- 모든 정점이 확정될 때까지 3-5단계를 반복한다.
예시
앞서 살펴봤던 그래프를 사용하여 다익스트라 알고리즘이 어떻게 작동하는지 살펴보자.
시작 정점을 A라고 가정하자.
-
초기 상태:
- d[A] = 0, d[B] = ∞, d[C] = ∞, d[D] = ∞, d[E] = ∞
- 모든 정점이 미확정 상태
-
A를 확정 상태로 표시하고, A의 인접 정점인 B와 C의 거리를 업데이트한다.
- d[B] = 8, d[C] = 5
-
미확정 정점 중에서 거리가 가장 짧은 C를 확정 상태로 표시하고, C의 인접 정점인 B, D, E의 거리를 업데이트한다.
- d[B] = 8, d[D] = 11, d[E] = 14
-
미확정 정점 중에서 거리가 가장 짧은 B를 확정 상태로 표시하고, B의 인접 정점인 D의 거리를 업데이트한다.
- d[D] = 9
미확정 정점 중에서 거리가 가장 짧은 D를 확정 상태로 표시하고, B의 인접 정점인 D의 거리를 업데이트한다.
- d[E] = 11
-
모든 정점이 확정되었으므로 알고리즘을 종료한다.
최종 결과:
- d[A] = 0, d[B] = 8, d[C] = 5, d[D] = 9, d[E] = 11
따라서 정점 A에서 각 정점까지의 최단 경로는 다음과 같다.
- A에서 B까지: A-B
- A에서 C까지: A-C
- A에서 D까지: A-B-D
- A에서 E까지: A-B-D-E
다익스트라 알고리즘: 정확성 증명과 시간 복잡도 분석
다익스트라 알고리즘의 정확성 증명
이번에는 다익스트라 알고리즘이 왜 항상 정확한 결과를 도출하는지 수학적으로 증명해보자.
증명을 위해 다음 두 가지 claim이 필요하다.
claim 1: 모든 정점 v에 대해, d[v] ≥ d(s, v) claim 2: 정점 v가 확정될 때, d[v] = d(s, v)
여기서 d[v]는 다익스트라 알고리즘에서 계산된 시작 정점 s에서 정점 v까지의 최단 경로 길이이고, d(s, v)는 실제 최단 경로 길이이다.
claim 1 증명 (귀납법)
- 기본 단계: 알고리즘 시작 시, d[s] = 0이고 d(s, s) = 0이므로 d[s] ≥ d(s, s)이다.
- 귀납 가정: 임의의 정점 u가 확정될 때까지 claim 1이 성립한다고 가정한다.
- 귀납 단계: 정점 u가 확정된 후, u의 인접 정점 v에 대해 d[v] = min(d[v], d[u] + w(u, v))로 업데이트된다. 귀납 가정에 의해 d[u] ≥ d(s, u)이고, 삼각 부등식에 의해 d(s, v) ≤ d(s, u) + w(u, v)이므로, d[v] ≥ d(s, v)이다.
따라서 모든 정점 v에 대해 d[v] ≥ d(s, v)이다.
주장 2 증명 (귀류법)
- 정점 v가 확정될 때 d[v] > d(s, v)라고 가정하자.
- d(s, v)는 s에서 v까지의 실제 최단 경로 길이이므로, 이 경로는 s에서 시작하여 v에서 끝나는 일련의 정점들로 구성된다.
- 이 경로에서 마지막으로 확정된 정점을 u, 그 다음 정점을 x라고 하자. 즉, 경로는 s, ..., u, x, ..., v와 같은 형태이다.
- u가 확정되었을 때, d[x] = d[u] + w(u, x)로 업데이트되었을 것이다.
- 주장 1에 의해 d[x] ≥ d(s, x)이고, u가 확정되었으므로 d[u] = d(s, u)이다. 따라서 d(s, x) ≤ d(s, u) + w(u, x)이다.
- 이는 s에서 x까지의 최단 경로가 s, ..., u, x임을 의미한다.
- x는 v보다 먼저 확정되어야 하지만, v가 먼저 확정되었다고 가정했으므로 모순이다.
따라서 정점 v가 확정될 때 d[v] = d(s, v)이다.
다익스트라 알고리즘의 시간 복잡도
다익스트라 알고리즘의 시간 복잡도는 다음과 같이 표현할 수 있다.
n(T(findMin) + T(removeMin)) + mT(updateKey)
여기서 n은 정점의 수, m은 간선의 수, T(findMin)은 최소 d[v] 값을 갖는 정점을 찾는 데 걸리는 시간, T(removeMin)은 해당 정점을 제거하는 데 걸리는 시간, T(updateKey)는 d[v] 값을 업데이트하는 데 걸리는 시간이다.
데이터 구조에 따라 시간 복잡도는 다음과 같이 달라진다.
| 데이터 구조 | T(findMin) | T(removeMin) | T(updateKey) | 전체 시간 복잡도 |
|---|---|---|---|---|
| 배열 | O(n) | O(1) | O(1) | O(n^2) |
| 레드-블랙 트리 | O(log n) | O(log n) | O(log n) | O(m log n) |
| 피보나치 힙 | O(1) | O(log n) | O(1) | O(m + n log n) |
다익스트라 알고리즘의 한계
다익스트라 알고리즘은 당장 눈앞의 최단 경로를 찾아가는, Greedy하고 Centralized된 알고리즘이다. 다음 시간에 벨만-포드 알고리즘에 대해 배우겠지만, 각각의 방식에 따라 trade-off가 존재한다. 다익스트라 알고리즘의 경우, 시간복잡도가 작은 대신, 다음과 같은 한계를 갖는다.
- 음수 가중치: 음수 가중치를 갖는 간선이 있는 경우 정확한 결과를 보장하지 않는다.
- 변경에 대한 취약성: 그래프의 가중치가 변경되면 알고리즘을 다시 실행해야 한다.
마치며
이번 포스팅에서는 다익스트라 알고리즘의 개념부터 예시, 그리고 알고리즘의 정확성을 증명하고, 시간 복잡도를 분석했다. 또한, 다익스트라 알고리즘의 한계점에 대해서도 알아보았다. 다익스트라 알고리즘은 가중치 그래프에서 최단 경로를 찾는 데 유용하게 사용되는 알고리즘이지만, 음수 가중치를 갖는 간선이 있는 경우에는 사용할 수 없다는 점에 유의해야 한다.
다음 시간에는 다익스트라 알고리즘과 대비되는 벨만-포드 알고리즘에 대해 알아보겠다.
추천글:
[알고리즘] Graph algorithm - Depth First Search, Topological ordering
(https://hyeondev.blogspot.com/2024/10/graph-algorithm-depth-first-search.html)
