[알고리즘] linear-time selection

Divide and Conquer II, 또다른 효율적인 알고리즘 : linear time selection(quick select)

서론

지난 시간에는 분할 정복 알고리즘의 대표적인 예시인 Merge Sort에 대해 알아보았다. Merge Sort를 이용하면 정렬된 리스트에서 k번째 작은 요소를 O(n log n) 시간에 쉽게 찾을 수 있다. 하지만 혹시 더 빠른 방법은 없을까? 정렬 없이도 k번째 작은 요소를 찾을 수 있다면, 시간 복잡도를 개선할 수 있지 않을까? 이러한 질문에서 시작된 탐구가 바로 linear time selection 알고리즘이다.

Linear time selection의 핵심 아이디어

선형 시간 선택 알고리즘의 핵심 아이디어는 다음과 같다:

피벗 선택: 리스트에서 하나의 요소를 피벗으로 선택한다.
분할: 피벗을 기준으로 리스트를 분할하여, 피벗보다 작은 요소들은 왼쪽, 큰 요소들은 오른쪽에 위치하도록 한다.
재귀: k번째 작은 요소가 어느 부분에 있는지 확인하고, 해당 부분 리스트에 대해 재귀적으로 알고리즘을 적용한다.

이 아이디어를 코드로 구현하면 다음과 같다.

Python
def quickselect(A, k):
  if len(A) == 1:
    return A[0]
  pivot = A[0]  # 단순화를 위해 첫 번째 요소를 피벗으로 선택
  left = [x for x in A[1:] if x < pivot]
  right = [x for x in A[1:] if x >= pivot]
  if k <= len(left):
    return quickselect(left, k)
  elif k == len(left) + 1:
    return pivot
  else:
    return quickselect(right, k - len(left) - 1)

이상적인 상황 -> O(n) 실행 시간

피벗이 매번 리스트를 정확히 절반으로 나눈다면, Quickselect 알고리즘의 실행 시간은 다음과 같은 점화식으로 표현된다.

T(n) = T(n/2) + O(n)

지난 시간에 알아본 마스터 정리를 이용하면, 이 점화식의 해는 T(n) = O(n)이다. 즉, 이상적인 상황에서는 선형 시간에 k번째 작은 요소를 찾을 수 있다.

정확성 증명: 수학적 귀납법

Quickselect 알고리즘의 정확성은 수학적 귀납법을 통해 증명할 수 있다. 귀납의 대상은 입력 리스트의 길이가 된다.

귀납 가설: 길이가 i인 입력 리스트에 대해 Quickselect는 k번째 작은 요소를 정확하게 찾는다.
기본 경우 (i=1): 길이가 1인 리스트에서는 k는 반드시 1이어야 하며, Quickselect는 유일한 요소를 반환하므로 성립한다.
귀납 단계: 길이가 1부터 i까지의 모든 리스트에 대해 Quickselect가 정확하게 동작한다고 가정하자. 길이가 i+1인 리스트에서 k번째 작은 요소를 찾는 경우를 생각해보자. 피벗을 기준으로 리스트를 분할하고, k가 왼쪽 부분 리스트에 속하는지, 피벗인지, 오른쪽 부분 리스트에 속하는지 판단한다. 각 경우에 대해 귀납 가설을 적용하면 Quickselect가 정확하게 k번째 작은 요소를 찾음을 알 수 있다.
결론: 수학적 귀납법에 의해, 임의의 길이 n에 대해 Quickselect는 k번째 작은 요소를 정확하게 찾는다.

최악의 경우 -> O(n^2) 실행 시간

피벗 선택이 잘못되어 매번 리스트가 거의 분할되지 않는 경우(ex. 1개만 나뉜 경우), Quickselect의 실행 시간은 다음과 같은 점화식으로 표현된다.

T(n) = T(n-1) + O(n)

이 점화식의 해는 T(n) = O(n^2)이다. 즉, 최악의 경우에는 Quickselect의 실행 시간이 quadratic하게 증가할 수 있다.

Median of Medians 알고리즘: 개선된 피벗 선택

최악의 경우를 피하기 위해서는 피벗을 잘 선택해야 한다. 이상적인 피벗은 리스트의 중앙값(median)이다. 하지만 현재까지 선형 시간에 중앙값을 찾는 알고리즘은 알려져 있지 않다. 따라서 중앙값에 근접한 값을 찾는 'Median of Medians' 알고리즘을 사용하여 피벗을 선택하는 방식으로 개선할 수 있다.

리스트를 5개씩 묶어 작은 그룹으로 나눈다.
각 그룹 내에서 중앙값을 찾는다. (Insertion Sort 등을 이용하여 O(1) 시간에 가능)
모든 그룹의 중앙값들을 모아 다시 Quickselect를 적용하여 중앙값을 찾는다. 이 값을 피벗으로 사용한다.

Median of Medians algorithm

Median of Medians 알고리즘 실행 시간 분석

Median of Medians 알고리즘의 실행 시간은 다음과 같은 점화식으로 표현된다.

T(n) = T(n/5) + T(7n/10) + O(n)

이는 n/5개의 그룹의 중앙값을 찾는 데 T(n/5), 7n/10개 이하의 요소들에 대해 재귀적으로 Quickselect를 적용하는 데 T(7n/10), 그리고 분할 및 기타 작업에 O(n)의 시간이 걸리기 때문이다. 이 점화식을 풀기 위해 귀납법을 사용할 수 있다. T(n) = O(n)이라고 가정하고, 이를 증명하면 Median of Medians 알고리즘의 실행 시간이 선형 시간임을 확인할 수 있다.

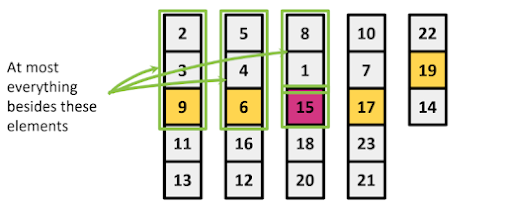n/5개 그룹 중 1/2의 그룹의 3개 요소(3n/10) - best case
best case의 반대(7n/10) - worst case

Median of Medians runtime

마무리

Linear time selection 알고리즘은 divide and conquer 패러다임을 활용하여 k번째 작은 요소를 효율적으로 찾는 알고리즘이다. 최악의 경우를 피하기 위해 Median of Medians 알고리즘을 사용하여 피벗을 선택하며, 이를 통해 평균적으로 선형 시간에 동작한다. 이 알고리즘은 정렬 없이도 특정 순위의 요소를 찾을 수 있으므로, 다양한 응용 분야에서 활용될 수 있다.

분할 정복은 복잡한 문제를 작은 문제로 나누어 해결하는, 어떤 문제를 해결할 때든 생각해보면 좋을 강력한 전략이다. 이런 면에서 Merge Sort와 Quickselect는 분할 정복의 다양한 활용 가능성을 보여주는 좋은 예시였다.

추천글 :

[알고리즘] Algorithmic Analysis - correctness with induction
(https://hyeonb.blogspot.com/2024/09/algorithmic-analysis-correctness-with.html)

[알고리즘] Algorithmic analysis - runtime with asymptotic analysis
(https://hyeonb.blogspot.com/2024/09/algorithmic-analysis-runtime-with.html)

[알고리즘] merge sort algorithm analysis
(https://hyeonb.blogspot.com/2024/09/merge-sort-algorithm-analysis.html)