Minimum Spanning Trees (MSTs)
지난 포스팅에서는 가중치 그래프(weighted graph)에서 최단 경로(shortest path)를 찾는 다익스트라 알고리즘(Dijkstra's algorithm)과 벨만-포드 알고리즘(Bellman-Ford algorithm)에 대해 알아보았다. 이번에는 가중치 그래프에서 또 다른 중요한 문제인 Minimum Spanning Tree (MST)에 대해 자세히 알아보겠다. MST는 그래프의 모든 정점을 연결하는 최소 비용의 트리 구조를 찾는 문제로, 네트워크 설계, 클러스터링, 이미지 분할 등 다양한 분야에서 활용된다.
1. MST란?
Spanning Subgraph
Spanning subgraph는 원래 그래프의 모든 vertex를 포함하는 부분 그래프다. 즉, 원래 그래프의 일부 간선을 제거하여 만든 그래프로, 모든 정점은 여전히 연결되어 있다.
Spanning Tree
Spanning tree는 spanning subgraph이면서 트리(cycle이 없는 연결된 그래프)인 그래프다. 즉, 그래프의 모든 정점을 연결하면서 사이클을 형성하지 않는 부분 그래프다.
Minimum Spanning Tree (MST)
Minimum Spanning Tree (MST)는 가중치 그래프에서 간선의 가중치 합이 최소인 spanning tree이다. MST는 여러 개 존재할 수 있으며, 통신 네트워크, 운송 네트워크 등 다양한 응용 분야에서 사용된다.
2. MST의 특징
2.1. Cycle Property
MST는 다음과 같은 Cycle Property를 만족한다.
MST T와 T에 포함되지 않는 간선 e가 있다고 가정하자. e를 T에 추가하면 사이클 C가 형성된다. 이때, C에 속하는 모든 간선 f에 대해 weight(f) ≤ weight(e)이다.
증명: 만약 weight(f) > weight(e)인 간선 f가 있다면, f를 e로 대체하여 더 작은 가중치를 갖는 spanning tree를 만들 수 있다. 이는 T가 MST라는 가정에 모순된다.
 |
| Cycle property |
2.2. Partition Property
MST는 다음과 같은 Partition Property를 만족한다.
그래프 G의 정점들을 두 개의 집합 U와 V로 분할한다. 이때, U와 V를 연결하는 간선 중 가중치가 가장 작은 간선 e는 반드시 MST에 포함된다.
증명: MST T가 간선 e를 포함하지 않는다고 가정하자. e를 T에 추가하면 사이클 C가 형성된다. C에는 U와 V를 연결하는 다른 간선 f가 반드시 존재하며, cycle property에 의해 weight(f) ≤ weight(e)다. 따라서 f를 e로 대체하여 또 다른 MST를 얻을 수 있으며, 이는 e가 MST에 포함됨을 의미한다.
 |
| Partition property |
3. MST 알고리즘
MST를 찾는 대표적인 알고리즘으로는 Prim-Jarnik 알고리즘과 Kruskal 알고리즘이 있다. 두 알고리즘 모두 탐욕 알고리즘(greedy algorithm)으로, 각 단계에서 최선의 선택을 하여 MST를 찾는다.
3.1. Prim-Jarnik's Algorithm
Prim-Jarnik 알고리즘은 Dijkstra's 알고리즘과 유사하게 작동한다. 임의의 정점 s에서 시작하여 MST를 점진적으로 확장해 나가는 방식이다.
(Dijkstra는 weight의 합이라면, Prim-Jarnik는 weight 값 그 자체로 설정)
- 시작 정점 s를 MST에 포함시키고, s에 인접한 정점들의 거리를 갱신
- MST에 포함되지 않은 정점 중 거리가 가장 짧은 정점 u를 MST에 추가
- 정점 u에 인접한 간선들을 이용하여 MST 외부에 있는 정점들의 거리를 갱신 (edge relaxation)
- 모든 정점이 MST에 포함될 때까지 2-3단계를 반복
 |
| Prim-Jarnik's algorithm example |
3.2. Kruskal's Algorithm
Kruskal 알고리즘은 간선을 가중치 순으로 정렬하고, 사이클을 형성하지 않는 선에서 간선들을 차례로 MST에 추가하는 방식이다.
- 그래프의 모든 간선을 가중치 순으로 오름차순 정렬
- 가장 작은 가중치를 가진 간선부터 MST에 추가해도 사이클이 형성되지 않으면 MST에 추가
- 모든 간선을 처리할 때까지 2단계를 반복
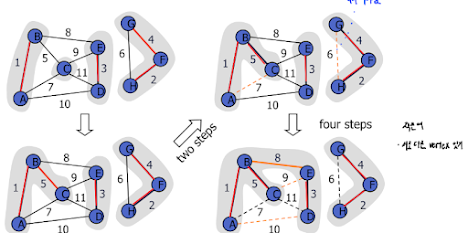 |
| Kruskal's algorithm example |
마무리
이번 포스팅에서는 MST의 개념, 특징, 그리고 대표적인 알고리즘인 Prim-Jarnik 알고리즘과 Kruskal 알고리즘에 대해 알아보았다. MST는 네트워크, 인공지능 등에서 활용되는 중요한 개념이므로, 이번 포스팅에서 다룬 내용들을 잘 이해하고 기억하는 것이 중요하다. 1학기가 끝나가는 지금.. 이제 자료구조에서 배울 내용도 얼마 남지 않았다!
추천글 :
[자료구조] Directed graph - Floyd-Warshall Transitive Closure, Topological sorting
(https://hyeonb.blogspot.com/2024/06/directed-graph-floyd-warshall.html)
[자료구조] Weighted graph & Dijkstra's algorithm
(https://hyeonb.blogspot.com/2024/06/weighted-graph-dijkstras-algorithm.html)

