[기계학습개론] Unsupervised learning technique - Clustering methods(Hierarchical clustering, K-means clustering, Gaussian Mixture Model, Spectral clustering)

비지도 학습 - 클러스터링 기법 파헤치기

오늘은 비지도 학습의 핵심이라 할 수 있는 클러스터링(Clustering) 기법들을 심층적으로 분석하고, 각 알고리즘의 작동 원리를 이해하는 시간을 가져보려 한다. 대규모 데이터셋 속에 숨겨진 패턴을 발견하는 데 필수적인 네 가지 방법론 – 계층적 클러스터링 (Hierarchical Clustering), K-평균 클러스터링 (K-means Clustering), 가우시안 혼합 모델 (Gaussian Mixture Model, GMM), 그리고 스펙트럴 클러스터링 (Spectral Clustering) – 의 이론적 기초부터 전문적인 응용까지 면밀히 살펴보겠다. 이 기법들은 뉴스 기사 주제 분류, 유전자 기능별 그룹화, 소셜 네트워크 사용자 관심사 분석 등 다방면에 활용되고있다는 점에서 그 중요성이 매우 크다.

1. 계층적 클러스터링 (Hierarchical Clustering): 데이터의 숨겨진 계층 구조 찾기

계층적 클러스터링은 데이터 포인트들 간의 유사성을 기반으로 계층적인 트리 구조, 즉 덴드로그램(Dendrogram)을 생성하는 방법이다. 데이터 자체가 자연스러운 계층을 이루고 있거나, 분석 목적에 따라 다양한 수준의 클러스터 해상도가 필요할 때 매우 유용하다.

Dendrogram

주요 접근 방식은 다음과 같이 두 가지로 나뉜다.

하향식 (Top-down, Divisive): 전체 데이터를 하나의 거대한 클러스터로 간주하고 시작하여, 점진적으로 더 작은 부분집합으로 나누어 내려가는 방식이다. 각 단계에서 생성된 부분집합에 대해 재귀적으로 클러스터링을 수행한다.
Top-down
상향식 (Bottom-up, Agglomerative): 각 데이터 포인트를 개별적인 클러스터로 간주하고 시작하여, 매 단계에서 가장 "가까운" 두 클러스터를 반복적으로 병합해 나가는 방식이다. 본 글에서는 이 상향식 접근법에 더 초점을 맞추고자 한다.
Bottom-Up

상향식 계층적 클러스터링에서 핵심은 클러스터 간의 "가까움", 즉 유사도(Similarity) 또는 거리(Distance)를 어떻게 정의하느냐이다. 이를 연결 방식(Linkage Method)이라고 하며, 대표적인 방법은 다음과 같다.

단일 연결 (Single Linkage): 두 클러스터 A와 B 사이의 거리를 두 클러스터에 속한 모든 데이터 포인트 쌍 (x,x′) 간의 거리 중 최솟값으로 정의한다.
Single linkage method

이는 마치 그래프에서 두 클러스터를 연결하는 가장 짧은 간선(edge)의 길이를 찾는 것과 유사하다. 특정 거리 임계값 r보다 가까운 모든 점들을 연결했을 때 나타나는 연결 요소(connected components)를 클러스터로 간주할 수 있다. 이 방식은 길고 늘어진 형태의 클러스터를 잘 찾아낼 수 있지만, '연쇄 효과(chaining effect)'로 인해 서로 다른 클러스터가 하나의 긴 클러스터로 합쳐지는 경향이 있다.

완전 연결 (Complete Linkage): 두 클러스터 A와 B 사이의 거리를 두 클러스터에 속한 모든 데이터 포인트 쌍 (x,x′) 간의 거리 중 최댓값으로 정의한다.
Complete linkage method

이는 클러스터의 최대 직경(diameter)을 가능한 작게 유지하려는 경향이 있어, 비교적 동그랗고 밀집된 클러스터를 형성한다. 단일 연결과는 반대로, 이상치(outlier)에 민감하게 반응할 수 있다.

평균 연결 (Average Linkage): 두 클러스터 A와 B 사이의 거리를 두 클러스터에 속한 모든 데이터 포인트 쌍 (x,x′) 간의 거리의 평균으로 정의한다.
dist(A,B)=avg dist(x,x′)
단일 연결과 완전 연결의 절충안으로 볼 수 있으며, 비교적 안정적인 클러스터링 결과를 제공한다.

이러한 연결 방식들을 적용하기 위해서는 먼저 개별 객체 쌍 간의 거리 측정이 선행되어야 한다. 이 거리 측정은 분석 대상 데이터의 도메인 특성에 따라 다양하게 정의될 수 있으며, 예를 들어 공통 키워드의 수, 문자열 간의 편집 거리(edit distance), 시계열 데이터의 웨이블릿 계수(wavelet coefficients) 등이 사용될 수 있다.

2. K-평균 클러스터링 (K-means Clustering): 데이터 중심을 찾아 효율적으로 분할하기

K-평균 클러스터링은 주어진 데이터 포인트들을 미리 정해진 K개의 클러스터로 분할하는 가장 대표적이고 널리 사용되는 알고리즘 중 하나이다. 알고리즘의 목표는 각 클러스터의 중심(centroid)과 해당 클러스터에 할당된 데이터 포인트들 간의 거리 제곱의 합, 즉 왜곡(distortion) 또는 응집도(inertia)를 최소화하는 것이다.

최적화하려는 목적 함수 J (왜곡)는 다음과 같이 표현된다.

objective function

여기서 K는 클러스터의 개수, Cj는 j번째 클러스터를 나타내고, x(i)는 i번째 데이터 포인트를, μj는 j번째 클러스터의 중심점을 의미한다. ∣∣⋅∣∣^2은 일반적으로 유클리드 거리의 제곱을 나타낸다.

알고리즘은 다음의 두 단계를 반복적으로 수행하며 최적의 클러스터 할당을 찾아간다.

할당 단계 (Assignment Step, E-step과 유사): 현재 각 클러스터의 중심 μj가 주어졌다고 가정하고, 각 데이터 포인트 x(i)를 가장 가까운 클러스터 중심에 할당한다. 즉, x(i)는 $j = argmin_{k} ∣∣ x^{(i)} - μ_{k} ∣ ∣^^{2}$ 를 만족하는 클러스터 j에 속하게 된다. 이 할당 정보를 c(i)로 표현할 수 있다. 이 단계는 현재 모델 파라미터(중심)가 고정된 상태에서 데이터 포인트의 최적 클러스터 소속 확률(여기서는 확정적 할당)을 찾는 과정으로, EM 알고리즘의 E-step(Expectation step)과 유사한 역할을 한다.
업데이트 단계 (Update Step, M-step과 유사): 각 클러스터에 데이터 포인트들이 할당된 상태에서, 각 클러스터 j의 새로운 중심 μj를 해당 클러스터에 속한 모든 데이터 포인트들의 평균으로 업데이트한다.
μj=∣Cj∣∑x(i)
여기서 ∣Cj∣는 클러스터 j에 속한 데이터 포인트의 개수이다. 이 단계는 데이터 포인트의 클러스터 할당이 고정된 상태에서 모델 파라미터(중심)를 업데이트하여 목적 함수를 최소화하는 과정으로, EM 알고리즘의 M-step(Maximization step)과 유사한 역할을 한다.
(EM 알고리즘의 자세한 내용은 아래 GMM에서 설명하겠다.)

K-means summary

이 두 단계는 데이터 포인트들의 클러스터 할당에 더 이상 변화가 없거나, 목적 함수 J의 감소량이 매우 작아질 때까지 반복된다. 각 반복 단계는 목적 함수 J의 값을 감소시키거나 유지시키므로 알고리즘의 수렴은 보장된다. 하지만, K-평균 알고리즘은 일반적으로 전역 최솟값(global minimum)이 아닌 지역 최솟값(local minimum)으로 수렴할 수 있다는 한계점을 가진다.

초기 클러스터 중심(K개)을 어떻게 선택하느냐가 최종 클러스터링 결과에 큰 영향을 미친다. 가장 간단한 방법은 훈련 데이터셋에서 무작위로 K개의 데이터 포인트를 선택하여 초기 중심으로 사용하는 것이다. 지역 최솟값 문제에 대처하기 위한 실무적인 접근법으로는, 서로 다른 초기 중심들로 알고리즘을 여러 번(예: 50~100회) 실행하고, 그중에서 가장 낮은 왜곡 값 J를 갖는 클러스터링 결과를 최종 결과로 선택하는 방식이 널리 사용된다(monte-carlo algorithm). K-means++와 같은 좀 더 지능적인 초기 중심 선택 방법도 존재한다.

K-평균 알고리즘은 유클리드 거리를 기반으로 하기 때문에 클러스터가 구형(spherical) 또는 초구형(hyperspherical)의 형태를 가질 때 좋은 성능을 보인다. 하지만, 범주형 데이터에는 직접 적용하기 부적절하며, 이상치(outliers)에 민감하게 반응하여 클러스터 중심이 왜곡될 수 있다는 단점이 있다. 이러한 단점을 보완하기 위해 중심점과의 L1 거리(맨해튼 거리)를 최소화하는 K-중앙값(K-median) 클러스터링이나, 최대 클러스터 반경을 최소화하는 K-중심(K-center) 클러스터링과 같은 변형된 알고리즘들이 제안되기도 했다.

K-평균 알고리즘의 대표적인 응용 사례로는 이미지 분할(Image Segmentation)이 있다. 이미지의 각 픽셀을 RGB (또는 다른 색 공간) 값으로 표현되는 하나의 데이터 포인트로 간주하고, K-평균 클러스터링을 적용하면 픽셀들을 K개의 그룹으로 묶어 이미지를 분할할 수 있다. 이는 각 클러스터의 중심 색상으로 해당 클러스터의 픽셀들을 대표하는 방식으로 이미지의 색상 수를 줄이는 효과를 가져온다.

또한, 손실 압축(Lossy compression)의 일종인 벡터 양자화(Vector Quantization)에도 활용된다. N개의 데이터 포인트 각각에 대해, 해당 포인트가 속한 클러스터의 중심 ID(k)만을 저장하고, K개의 클러스터 중심값들은 별도의 코드북(code-book)으로 저장한다 (일반적으로 $K ≪ N$ ). 예를 들어, 각 픽셀이 24비트(RGB 각각 8비트)로 표현되는 이미지에서 N개의 픽셀이 있고, 이를 $K = 10$ 개의 클러스터로 양자화한다면, 원본 데이터는 24N 비트가 필요하지만, 압축된 데이터는 K개의 중심 색상을 저장하는 데 24K 비트, 각 픽셀이 어떤 중심에 해당하는지 저장하는 데 Nlog2K 비트가 필요하여 상당한 압축률을 얻을 수 있다. (예시: $24 K + N lo g_{2} K$ 비트. $K = 10$ 일 때 $lo g_{2} 10 \approx 3.32$ 이므로, 대략 $240 + 3.32 N$ 비트로 원본 24N 비트 대비 압축된다.)

3. 가우시안 혼합 모델 (Gaussian Mixture Model, GMM): 데이터 분포를 유연하게 모델링하기

가우시안 혼합 모델(GMM)은 전체 데이터 모집단이 실제로는 여러 개의 서로 다른 가우시안 분포(Gaussian distribution)를 따르는 하위 모집단(sub-population)들의 혼합으로 이루어져 있다고 가정하는 확률론적 모델이다. 이러한 모델을 데이터에 적합시키는 과정 자체가 비지도 학습 또는 클러스터링의 한 형태로 볼 수 있다. GMM은 단일 가우시안 분포로는 표현하기 어려운 복잡한 형태의 데이터 분포를 모델링하는 데 강력한 프레임워크를 제공하며, 데이터를 부드러운 경계로 클러스터링하는 데 사용된다.

GMM은 K개의 가우시안 컴포넌트(Gaussian components)의 선형 결합으로 데이터의 확률 밀도 함수(Probability Density Function, PDF) p(x)를 표현한다.

여기서,

$K $는 혼합 모델을 구성하는 가우시안 컴포넌트의 개수이다.
$\pi_{k} $는 k번째 가우시안 컴포넌트의 혼합 계수(mixing coefficient)로, $\Sigma \pi_{k} = 1$ 이고 $0 \leq \leq 1$ 이다. 이는 특정 데이터 포인트가 k번째 가우시안 분포에서 생성되었을 사전 확률(prior probability)로 해석될 수 있다.
N(x∣μ_k,Σ_k)는 k번째 가우시안 컴포넌트의 확률 밀도 함수이며, μ_k는 평균 벡터(mean vector), Σ_k는 공분산 행렬(covariance matrix)이다. 공분산 행렬은 클러스터의 모양, 방향성, 크기 등을 결정한다.

GMM의 목표는 주어진 데이터셋 {x1,…,xN}에 대해 최대 우도 추정(Maximum Likelihood Estimation, MLE)을 통해 모델 파라미터 세트 $θ = {π_{k}, μ_{k}, Σ_{k}}_{k = 1}^{K}$ 를 찾는 것이다. 즉, 로그 우도 함수 $ln p (X ∣ π, μ, Σ) = \sum ln (\sum π_{k} N (x_{n} ∣ μ_{k}, Σ_{k}))$ 를 최대로 하는 파라미터를 찾는 것이다. 그러나 이 로그 우도 함수는 합(summation) 기호가 로그 함수 내부에 있어 파라미터에 대한 닫힌 형태(closed-form)의 해를 직접 구하기 어렵다. 이러한 문제를 해결하기 위해 EM(Expectation-Maximization) 알고리즘이 널리 사용된다.

Maximum likelihood

EM 알고리즘은 관찰되지 않은 잠재 변수(latent variable) z를 도입하여 문제를 단순화한다. 각 데이터 포인트 $x_{n}$에 대해, K차원의 이진 랜덤 변수 $z_{n}$ $= (, \dots,$ $z_{nk}$ $)$ 를 가정하며, $\in {0, 1}$ 이고 $= 1$ 이다. 데이터 포인트 $x_{n} $이 k번째 가우시안 컴포넌트에서 생성되었음을 의미한다. $p ($ $z_{nk} = 1 $ $) =$ 로 정의되며, $x_{n} $은 관찰된 변수, $z_{n}$은 숨겨진(hidden) 또는 누락된(missing) 변수로 취급된다. 결합 분포 $p (x, z) = p (x ∣ z) p (z)$ 로 정의하고, 관찰 데이터의 우도 p(x)는 p(x,z)를 모든 가능한 z에 대해 주변화(marginalize)함으로써 얻어진다.

GMM을 위한 EM 알고리즘은 다음의 두 단계를 반복한다.

초기화 (Initialization): 평균 μk, 공분산 Σk, 혼합 계수 πk에 대한 초기값을 설정한다. (예: K-평균 결과를 사용하여 초기화) 그리고 초기 로그 우도 값을 계산한다.
E 단계 (Expectation Step): 현재 파라미터 값 (πk,μk,Σk)을 사용하여, 각 데이터 포인트 xn이 각 가우시안 컴포넌트 k에서 생성되었을 사후 확률(posterior probability), 즉 책임 값(responsibility) γ(znk)를 계산한다. 이 값은 k번째 컴포넌트가 데이터 포인트 xn을 생성하는 데 얼마나 "책임"이 있는지를 나타낸다.

posterior probability(responsibility)

M 단계 (Maximization Step): E 단계에서 계산된 책임 값 γ(znk)를 사용하여 모델 파라미터 (πk,μk,Σk)를 재추정한다. 이는 완전 데이터 로그 우도(complete-data log likelihood)의 기댓값을 최대화하는 파라미터를 찾는 과정이다.
새로운 평균 μk_new, 새로운 공분산 Σk_new, 새로운 혼합 계수 πk_new:
New parameter

여기서 Nk=∑γ(znk)는 k번째 클러스터에 효과적으로 할당된 데이터 포인트의 수로 해석될 수 있다.
수렴 확인 (Convergence Check): 로그 우도 lnp(X∣πnew,μnew,Σnew)를 평가하고, 이 값이 이전 단계의 로그 우도 값과 비교하여 변화가 거의 없거나 미리 정한 반복 횟수에 도달하면 알고리즘을 종료한다. 그렇지 않으면 E 단계로 돌아가 반복한다.

Entire process

GMM과 K-평균을 비교해 보면, K-평균은 각 데이터 포인트를 가장 가까운 클러스터 중심에 배타적으로 할당하는 하드 할당(hard assignment) 방식인 반면, GMM의 EM 알고리즘은 각 데이터 포인트가 모든 클러스터에 속할 확률(책임 값)을 계산하는 소프트 할당(soft assignment) 방식을 사용한다. 또한, K-평균은 클러스터의 중심(평균)만을 추정하는 데 비해, GMM은 클러스터의 평균과 함께 공분산 행렬까지 추정하여 클러스터의 다양한 모양(타원형 등)과 방향성을 모델링할 수 있다는 장점이 있다.

그러나 GMM은 K-평균에 비해 계산량이 많고, 수렴하는 데 더 많은 반복이 필요할 수 있다. 또한, EM 알고리즘은 로그 우도 함수의 지역 최댓값으로 수렴할 수 있으므로, 초기 파라미터 설정이 중요하며, K-평균 알고리즘을 먼저 실행하여 그 결과를 GMM의 초기 평균 및 공분산 행렬 값으로 사용하는 경우가 많다. GMM의 응용 사례로는 이미지의 전경과 배경을 분리하는 대화형 분할 알고리즘인 GrabCut 등이 있다.

K-means vs GMM

4. 스펙트럴 클러스터링 (Spectral Clustering): 그래프 기반의 비선형 구조 탐색

스펙트럴 클러스터링은 데이터를 저차원의 다른 특징 공간(feature space)으로 변환한 후 클러스터링을 수행하는 방법으로, 최근 그 효과와 유연성으로 인해 많은 주목을 받고 있다. 이 방법은 데이터 포인트들 간의 연결성 또는 유사성을 그래프(graph) 구조로 표현하고, 이 그래프의 스펙트럼(고유값 및 고유 벡터) 정보를 활용하여 클러스터를 찾는다. 특히, 복잡한 형태(예: 동심원, 나선형)의 클러스터나 서로 겹쳐 있는 클러스터와 같이 K-평균과 같은 전통적인 방법으로는 찾기 어려운 비선형적 구조를 가진 데이터를 효과적으로 분할할 수 있다.

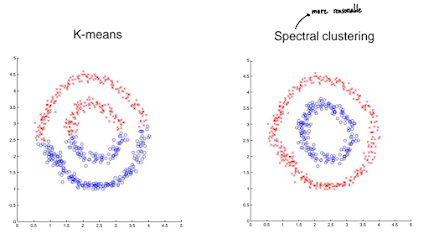Background of Spectral Clustering

핵심 아이디어는 다음과 같다.

유사도 그래프 구축 (Similarity Graph Construction): 데이터 포인트들을 정점(vertex)으로 하고, 포인트들 사이의 유사도(affinity) 또는 근접성(proximity)을 간선(edge)의 가중치로 하는 그래프를 생성한다. 유사도는 유클리드 거리 기반의 가우시안 유사도 함수 등을 사용할 수 있다. 그래프는 모든 가능한 쌍을 연결하는 완전 연결 그래프(fully connected graph)로 만들거나, 각 포인트에서 가장 가까운 k개의 이웃만을 연결하는 K-최근접 이웃 그래프(K-nearest neighbor graph), 또는 특정 거리 ϵ 내의 이웃만을 연결하는 $ϵ$ -이웃 그래프( $ϵ$ -neighborhood graph) 등으로 구성할 수 있다. 이 단계에서 생성된 가중치 인접 행렬(weighted adjacency matrix)을 W라고 하자 (W_ij는 정점 i와 j 사이의 유사도).
affinity
라플라시안 행렬 계산 (Laplacian Matrix Computation): 그래프 W로부터 라플라시안 행렬(Laplacian matrix) L을 계산한다. 라플라시안 행렬은 그래프의 구조적 특성을 담고 있으며, 여러 형태로 정의될 수 있다.
- 비정규화 라플라시안 (Unnormalized Laplacian): $L = D - W$ 여기서 D는 차수 행렬(degree matrix)로, 대각 성분 $D__{ii} = \sum W__{ij}$ (정점 i에 연결된 모든 간선의 가중치 합)이고 나머지 성분은 0인 대각 행렬이다.
- 정규화 라플라시안 (Normalized Laplacian):
  - 대칭 정규화 라플라시안 (Symmetric normalized Laplacian): $L_{sy m} = D^{- 1/2} L D^{- 1/2} = I - D^{- 1/2} W D^{- 1/2}$
  - 랜덤 워크 정규화 라플라시안 (Random walk normalized Laplacian): $L_{r w} = D^{- 1} L = I - D^{- 1} W$ 일반적으로 정규화된 라플라시안, 특히 Lsym이나 Lrw가 더 좋은 성능을 보이는 경우가 많다.
고유값 분해 및 특징 벡터 선택 (Eigen-decomposition and Feature Vector Selection): 계산된 라플라시안 행렬 L (또는 Lsym, Lrw)에 대해 고유값 분해(eigen-decomposition)를 수행하여 고유값(eigenvalue)과 그에 해당하는 고유 벡터(eigenvector)를 찾는다. 클러스터링을 위해 K개의 가장 작은 (또는 특정한) 고유값에 해당하는 K개의 고유 벡터를 선택한다. (비정규화 라플라시안과 Lsym의 경우 작은 고유값, Lrw의 경우 1에 가까운 고유값들을 고려하기도 하지만, 일반적으로는 가장 작은 K개의 고유값에 대응하는 고유 벡터들을 사용한다. 특히, 정규화된 컷 관점에서는 두 번째로 작은 고유값에 해당하는 고유 벡터부터 사용된다.) 이 K개의 고유 벡터들을 열(column)로 하는 새로운 행렬 $U \in R^{N \times K}$ 를 구성한다. 이 행렬의 각 행(row) $y__{i} \in R^{K}$ 는 원래 데이터 포인트 x_i를 새로운 K차원 특징 공간으로 매핑한 결과로 볼 수 있다.
새로운 특징 공간에서 클러스터링 (Clustering in the New Feature Space): 이렇게 얻어진 N개의 새로운 K차원 특징 벡터 {y_1,…,y_N}에 대해 K-평균 클러스터링과 같은 간단한 클러스터링 알고리즘을 적용하여 K개의 클러스터로 분할한다.

스펙트럴 클러스터링의 근본적인 아이디어는 그래프를 K개의 서로소 부분 그래프(disjoint subgraphs)로 나누되, 서로 다른 부분 그래프를 연결하는 간선들의 가중치 합(컷, cut)은 최소화하고, 각 부분 그래프 내부의 간선들의 가중치 합은 최대화하는 그래프 컷(Graph Cut) 문제와 관련이 깊다. 단순한 컷(MinCut)은 종종 불균형한 크기의 클러스터를 생성하는 경향이 있어, 이를 보완하기 위해 클러스터의 크기를 고려하는 정규화된 컷(Normalized Cut, Ncut) 또는 비율 컷(Ratio Cut)과 같은 개념이 도입되었다.

이 Ncut 문제를 푸는 것은 NP-hard 문제로 알려져 있으며, 스펙트럴 클러스터링은 이 문제의 근사해를 라플라시안 행렬의 고유 벡터를 통해 찾는 방법이다. 특히, K=2인 경우, 두 번째로 작은 고유값에 해당하는 고유 벡터(Fiedler vector)가 Ncut 문제의 좋은 근사 해를 제공한다고 알려져 있다.

구현은 비교적 간단할 수 있지만, 왜 이 방법이 비선형 구조를 잘 찾아내는지에 대한 이론적 배경은 그래프 이론, 선형 대수, 행렬 섭동 이론 등과 연관되어 다소 복잡할 수 있다. 그럼에도 불구하고, 적절한 유사도 정의와 라플라시안 선택을 통해 다양한 형태의 클러스터를 효과적으로 구분해낼 수 있다는 점에서 강력한 방법론이다.

Spectral Clustering examples

결론: 데이터의 특성에 맞는 최적의 클러스터링 전략은 따로 있다

지금까지 계층적 클러스터링, K-평균 클러스터링, 가우시안 혼합 모델, 그리고 스펙트럴 클러스터링이라는 네 가지 주요 클러스터링 기법들의 핵심 원리와 작동 방식, 그리고 응용 분야에 대해 깊이 있게 살펴보았다. 각 방법론은 데이터의 내재적 특성, 우리가 찾고자 하는 클러스터의 구조, 허용 가능한 계산 복잡성, 그리고 최종 결과의 해석 방식 등에 따라 고유한 장단점과 적합한 적용 범위를 가진다.

계층적 클러스터링은 데이터의 숨겨진 계층 구조를 탐색하고 다양한 수준의 클러스터링 결과를 얻고자 할 때 유용하다.
K-평균 클러스터링은 계산 효율성이 뛰어나 대규모 데이터에 빠르게 적용 가능하지만, 클러스터가 구형이라고 가정하며 초기 중심 선택과 이상치에 민감하다.
가우시안 혼합 모델은 데이터의 확률 분포를 모델링하여 클러스터 간의 중첩을 허용하고 클러스터의 다양한 모양을 고려할 수 있지만, EM 알고리즘의 수렴 문제와 계산 비용이 고려되어야 한다.
스펙트럴 클러스터링은 그래프 이론을 활용하여 복잡하고 비선형적인 구조의 클러스터를 찾는 데 강력하지만, 이론적 배경이 다소 복잡하고 유사도 그래프 구축 방식에 따라 성능이 달라질 수 있다.

실무에서는 이러한 클러스터링 기법들을 단독으로 사용하기보다는, 데이터의 특성을 면밀히 분석하고 해결하고자 하는 문제의 구체적인 요구사항에 맞춰 적절한 기법을 선택하거나 여러 기법을 조합하는 지혜가 필요하다. 예를 들어, GMM의 초기 파라미터 설정을 위해 K-평균 결과를 활용하거나, 서로 다른 클러스터링 기법의 결과를 앙상블하여 더 강건한 클러스터링 결과를 도출할 수도 있다.

[기계학습개론] Supervised learning technique - Decision tree & Ensemble