[인공지능개론] information based learning - Shannon's entropy model

결정 트리 심화 : Shannon 엔트로피 모델을 이용한 정량적 접근

Shannon 엔트로피 모델: 불확실성을 측정하는 척도

지난 시간에는 결정 트리의 개념과 정보 이득의 중요성에 대해 알아보았다. 이번 시간에는 결정 트리를 보다 정량적으로 분석하기 위해 Shannon 엔트로피 모델을 도입한다. Shannon 엔트로피는 정보 이론에서 불확실성을 측정하는 척도로, 어떤 사건이 발생할 확률이 낮을수록 엔트로피가 높아진다. 즉, 예측하기 어려울수록 엔트로피 값이 커지는 것이다.

카드 게임으로 이해하는 엔트로피

카드 게임을 예시로 들어보자. 52장의 카드 중에서 임의로 한 장을 뽑았을 때, 그 카드가 어떤 카드인지 맞추는 것은 매우 어렵다. 즉, 불확실성이 높은 상태이며, 따라서 엔트로피 값이 높다. 반대로, 카드 뭉치에서 빨간색 카드 26장만 남았을 때 빨간색 카드를 뽑을 확률은 100%이므로 불확실성이 낮고 엔트로피 값도 낮다.

entropy

엔트로피 계산: 로그 함수를 이용한 정량화

엔트로피는 다음과 같은 공식으로 계산한다.

H(X) = - Σ p(x) log₂p(x)

여기서 X는 확률 변수, p(x)는 X가 특정 값 x를 가질 확률이다.

로그 함수를 사용하는 이유는 각 사건의 정보량을 더할 때, 독립적인 사건들의 정보량이 곱해지도록 하기 위해서이다. 예를 들어, 동전을 두 번 던져 앞면이 두 번 나올 확률은 1/2 * 1/2 = 1/4 이다. 각 동전 던지기의 정보량을 1이라고 하면, 두 번 던져 앞면이 두 번 나올 사건의 정보량은 1 + 1 = 2가 된다. 이를 확률로 표현하면 log₂(1/4) = -2 이므로, 로그 함수를 사용하면 정보량을 확률의 로그 값으로 나타낼 수 있다. (부호는 -를 곱하여 +로 만든다)

한편, 이를 통해 엔트로피 값의 의미에 대해 생각해볼 수 있다. 동전을 여러번 던질수록, 정보량이 많아지며 엔트로피가 커진다. 즉, 엔트로피 값이 높다는 것은 불확실성이 높다는 것을 의미하며, 따라서 예측이 어렵다는 것을 뜻한다. 반대로 엔트로피 값이 낮다는 것은 불확실성이 낮다는 것을 의미하며, 예측이 쉽다는 것을 뜻한다.

정보 이득: 불확실성 감소량

정보 이득은 특정 설명 변수를 사용하여 데이터를 분류했을 때, 엔트로피가 얼마나 감소하는지를 나타내는 척도이다. 정보 이득이 높을수록 해당 변수가 데이터를 효과적으로 분류하는 데 유용하다는 것을 의미한다.

정보 이득 계산: 3단계 프로세스

정보 이득은 다음과 같은 3단계 프로세스를 통해 계산한다.

전체 데이터셋의 엔트로피 계산: 전체 데이터셋의 엔트로피를 계산한다.
설명 변수를 기준으로 데이터 분할: 특정 설명 변수를 기준으로 데이터를 여러 개의 부분 집합으로 나눈다.
각 부분 집합의 엔트로피 계산 및 가중 평균: 각 부분 집합의 엔트로피를 계산하고, 각 부분 집합의 크기를 가중치로 사용하여 가중 평균을 구한다.
정보 이득 계산: 전체 데이터셋의 엔트로피에서 가중 평균 엔트로피를 뺀 값이 정보 이득이다.

information gain formula

이메일 스팸 예측: 정보 이득 계산 예시

이메일 스팸 예측 모델을 예시(지난 시간 참조)로 들어보자. '의심스러운 단어 포함 여부'라는 설명 변수를 사용하여 데이터를 분류한다고 가정하자.

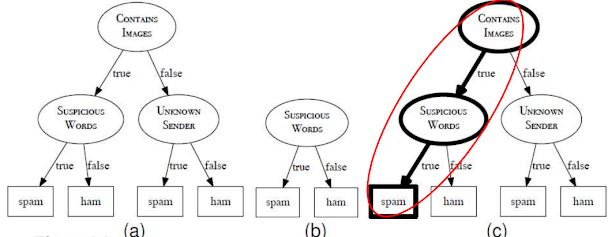email spam prediction model

전체 데이터셋의 엔트로피를 계산한다.
total entropy
'의심스러운 단어 포함' 그룹과 '의심스러운 단어 미포함' 그룹으로 데이터를 나눈다.
각 그룹의 엔트로피를 계산하고, 각 그룹의 크기를 가중치로 사용하여 가중 평균을 구한다.
remaining entropy
전체 데이터셋의 엔트로피에서 가중 평균 엔트로피를 뺀 값이 '의심스러운 단어 포함 여부' 변수의 정보 이득이다.
information gain

결정 트리 구축: 정보 이득 기반 변수 선택

결정 트리를 구축할 때, 각 노드에서 정보 이득이 가장 높은 설명 변수를 선택하여 분할 기준으로 사용한다. 이 과정을 반복하여 트리를 성장시키며 모든 leaf 노드가 순수해질 때까지 분할이 진행된다. 이때 순수 노드는 해당 노드에 속하는 모든 데이터가 같은 클래스에 속하는 노드를 의미한다.(구분 완료된 상태)

가지치기: 과적합 방지

결정 트리가 과도하게 성장하면 과적합 문제가 발생할 수 있다. 이를 방지하기 위해 가지치기(pruning) 기법을 사용한다. 가지치기는 트리의 일부 가지를 제거하여 트리의 복잡도를 줄이는 방법이다.(자세한 내용은 기회가 있다면 다뤄보겠다)

결론: 정보 이득 기반 결정 트리

Shannon 엔트로피 모델을 이용하여 정보 이득을 정량적으로 계산하고, 이를 기반으로 결정 트리를 구축할 수 있다. 정보 이득이 높은 설명 변수를 선택하여 트리를 성장시키고, 가지치기를 통해 과적합을 방지하면 예측 성능이 우수한 결정 트리 모델을 얻을 수 있다.

추천글 :
[인공지능개론] Artificial Intelligence Basics
(https://hyeonb.blogspot.com/2024/09/artificial-intelligence-basics.html)

[인공지능개론] information based learning - Decision tree

(https://hyeonb.blogspot.com/2024/10/information-based-learning-decision-tree.html)